1. 서론
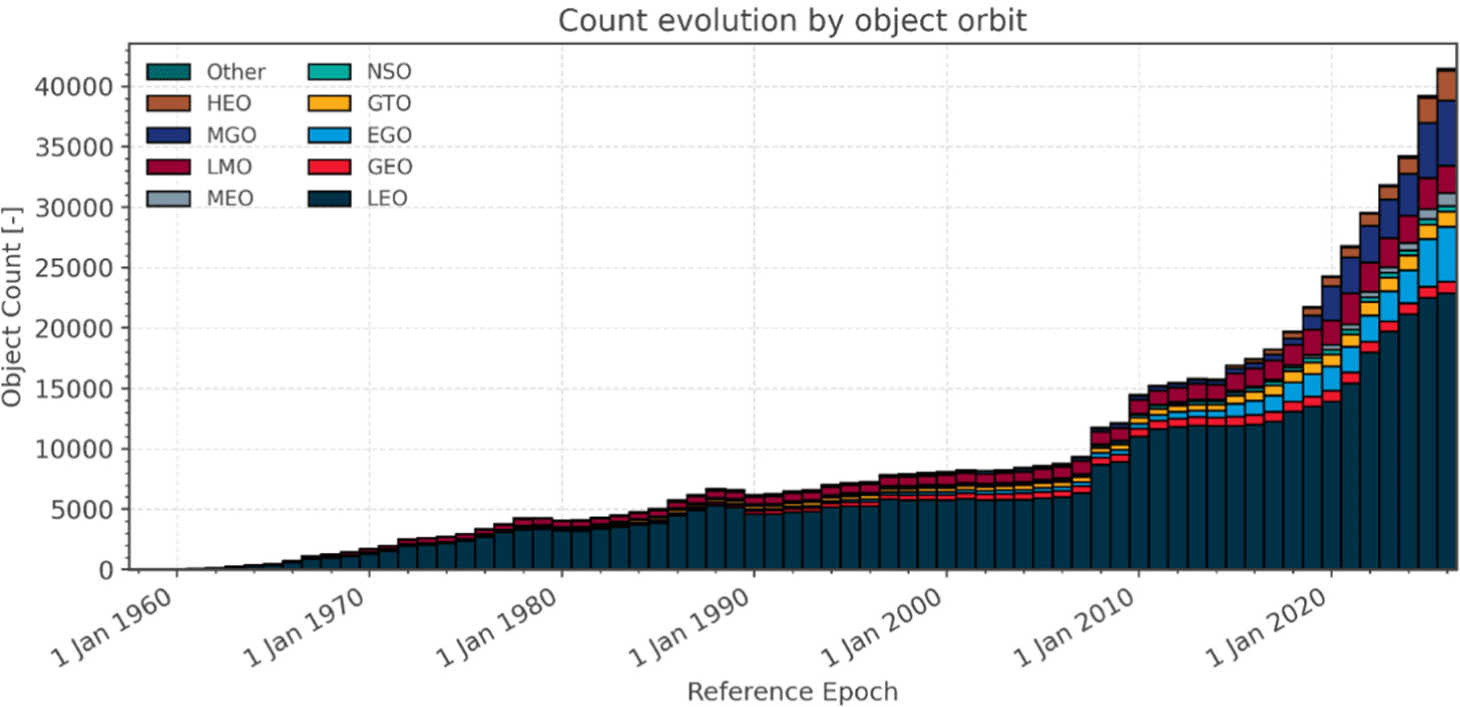
최근 재사용 발사체, 라이드 셰어링 등 발사 서비스‧기술의 발전이 우주공간의 접근성을 높이면서, 민간 영역에서 군에 이르기까지 우주활동이 급격하게 증가하고 있다. 정지궤도(geo-stationary earth orbit) 는 특수한 궤도 특성으로 이전부터 지구관측 및 통신 임무 등에 활발하게 이용되고 있으며, 지구 저궤도(low earth orbit, LEO)에서는 최근 다양한 우주 임무 수행의 가능성과 용이한 접근성 등의 이점으로 활용이 눈에 띄게 증가하고 있다. 특히, 발사 비용의 감소, 전자 부품의 소형화와 우주 운용 기술의 고도화가 적게는 수십에서 많게는 수만 개의 위성이 군집을 이루어 운용하는 위성군 개념을 보편화 하면서, 저궤도환경을 더욱 더 빠르게 혼잡하게 만들고 있다. Fig. 1은 ESA(European Space Agency)’s Space Debris Office에서 매년 발표하는 Space Environment Statistics에서 발췌한 그래프로, 운용궤도별 우주물체 수의 변화 추이를 보여준다.
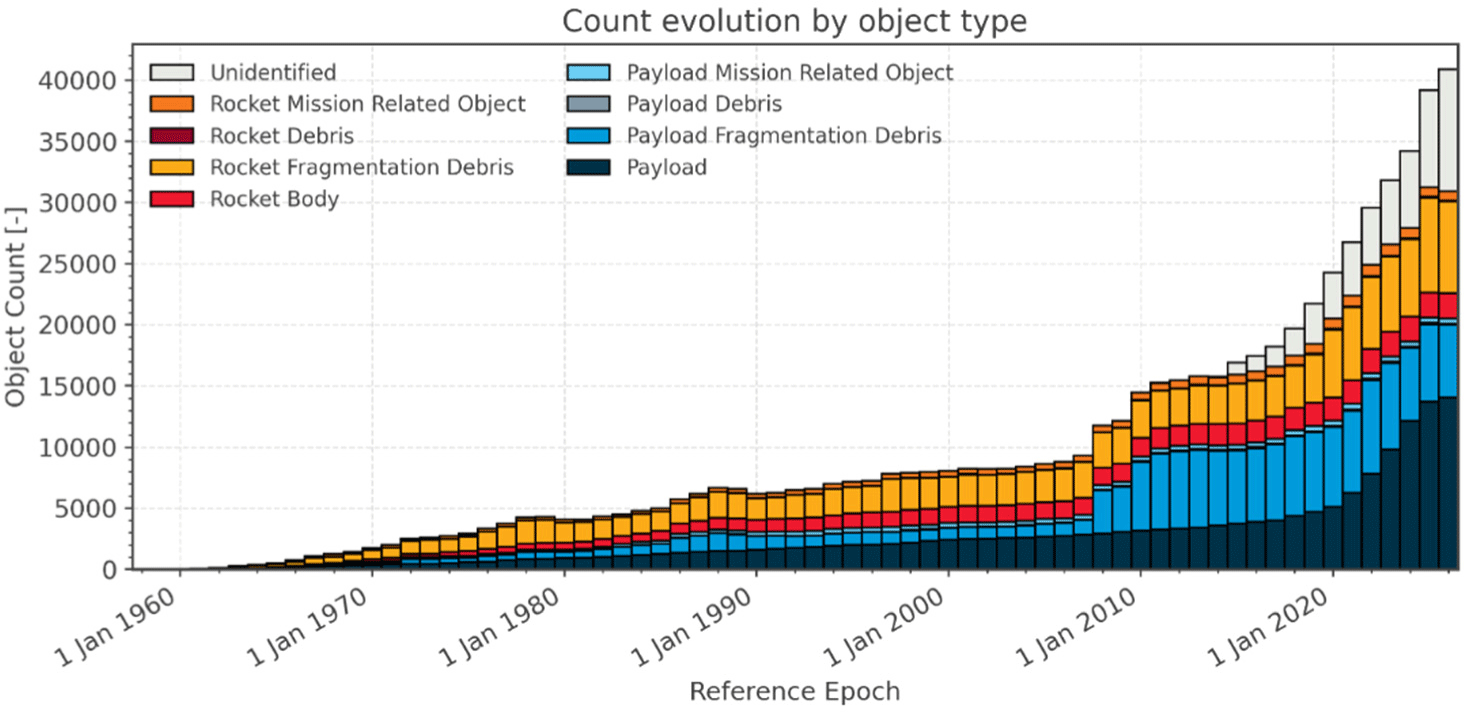
우주물체 간 충돌(collision), 폭발(explosion), 고의적 행위(deliberate acts), 추진(pro-pulsion) 등으로 발생하는 파편화 역시 우주물체의 수를 늘리는 주요 요인이다. ESA에 따르면 지금까지 650회 이상의 충돌 및 폭발 등의 파편화 이벤트가 발생한 것으로 추정되며, 2024년에는 총 10회의 파편화 이벤트가 관측되었다[2]. 우주물체 간 충돌의 대표적인 사례로는 2009년 2월 시베리아 상공 약 800 km 부근에서 발생한 미국의 통신 위성 Iridium 33과 러시아의 군 통신 위성 Cosmos 2251 간의 충돌이 있으며, 이로 인해 약 2,000개의 파편이 생성되었다[3]. 이와 비슷한 규모의 파편 생성은 위성 공격, 즉 anti-satellite weapon(ASAT) 실험으로도 발생했다. 2007년 중국의 ASAT 실험에서는 기상위성 FY-1C를 미사일로 요격해 3,000개 이상의 파편을 남겼으며[4], 최근인 2021년 러시아의 Cosmos-1408 위성 요격 실험에서도 1,800개 이상의 파편이 발생했다[5]. 이러한 파편화 사건들은 임무 후 폐기(post-mission disposal) 등 추가적인 대응책이 없다면 우주활동이 증가할수록 자연스럽게 증가할 수밖에 없는 상황이다. Fig. 2는 유형별로 분류한 우주물체 수의 변화 양상을 보여준다.
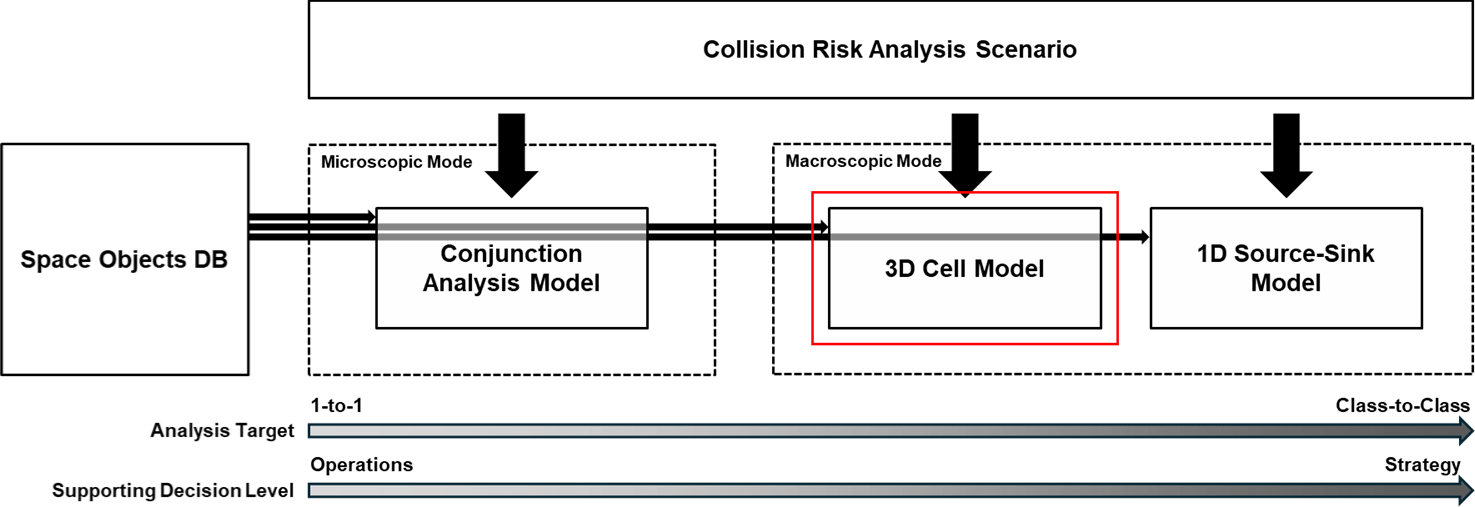
이와 같은 활발한 우주 개발과 우주물체의 파편화로 인해 근지구 우주 환경은 점점 복잡해지고 있으며, 이에 따라 우주상황인식(space situational awareness, SSA)에 대한 관심이 높아지고 있다. SSA는 지상 및 우주 기반의 관측 장비를 통해 우주물체를 관측·분석하여 대응 활동을 수행하는 것으로, 우주 환경에 대한 포괄적인 지식 획득 및 이해를 의미한다. 이 가운데 우주 위험 분석 시스템은 관측 데이터를 분석해 우주물체 재진입 위험이나 근접 우주물체 간 충돌 확률을 계산함으로써 전체 우주 위험도를 평가한다. 우리나라는 우주위험대비 기본계획을 바탕으로 독자적인 우주 위험 분석 역량을 확보하기 위해 우주물체 관측 시스템과 우주 위험 통합 분석 시스템을 개발 중이다. 우주위험대비 통합분석시스템 개발 계획의 일환으로 우주 위험 통합 분석 시스템은 전략 단위부터 운용 단위에 이르기까지 다양한 의사결정을 지원하기 위해 우주자산의 충돌 위험 분석을 수행한다. 기존 연구에서 본 연구팀은 여러 우주 선진국들의 개발 및 운용 사례를 분석하여, 해당 시스템을 미시적 모드(microscopic mode)와 거시적 모드(macroscopic mode)의 서브 모듈로 구성하였으며, 거시적 모드는 다시 1D source-sink model과 3D cell model(3차원 셀 모델)로 구성하였다(Fig. 3)[6–8].
본 연구에서는 우주 위험 통합 분석 시스템의 서브모듈 중 하나인 3차원 셀 모델의 개발 내용을 다룬다(Fig. 3의 붉은색 박스). 해당 모델은 주어진 우주물체 환경에서 평균 충돌 확률을 계산할 수 있을 뿐만 아니라, 다양한 기능을 결합해 우주물체 환경 진화 시뮬레이션, 불확실한 요소를 고려한 충돌 시나리오 분석 등 다양한 의사결정을 지원할 수 있는 도구로 확장될 수 있다.
2장에서는 3차원 셀 모델 개발에 필요한 이론적 배경을 소개하며, 3장에서는 2장에서 소개한 내용을 토대로 개발된 모델을 ESA의 3차원 셀 모델인 MASTER-8.0.5와 비교·검증한다. 비교·검증을 위해 LEO에서의 우주물체 공간 밀도와 우리별(KITSAT) 1·2·3호에 대한 충돌 위험 계산 결과를 개발된 모델과 MASTER 모델의 결과로 비교·분석한다. 4장에서는 연구 내용을 정리하여 결론 및 향후 연구 방향을 제시한다.
2. 3차원 셀 모델
3차원 셀 모델은 충돌 위험 분석 대상 물체의 궤도가 통과하는 영역에 초점을 맞추어, 충돌 위험 물체들이 해당 영역에서 발생시키는 충돌 플럭스(impact flux)를 바탕으로 충돌 위험을 분석한다(CUBE model[9]). 관심 대상 물체의 충돌 확률을 계산하는 전체 과정은 다음 네 단계로 요약할 수 있다.
-
관심 영역을 지구중심 관성 좌표계(earth-centered inertial frame)에서 고도가 일정한 등고도면, 적위가 일정한 등위도면, 적경이 일정한 등경도면으로 분할하여 셀(cell) 구성
-
각 셀마다 충돌 위험 물체가 형성하는 공간 밀도(spatial density) 계산
-
계산된 공간 밀도에 기반하여 충돌 위험 분석 대상 물체의 궤도에 대한 충돌 플럭스(collision flux) 계산
-
계산된 충돌 플럭스에 기반하여 충돌 확률(collision probability) 계산
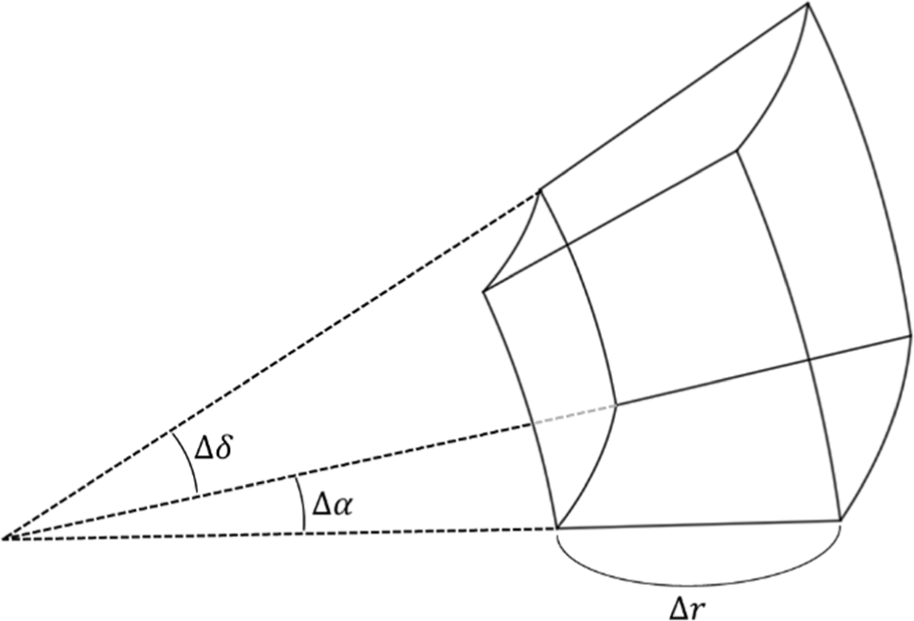
첫 번째 과정은 분석공간을 구면 좌표계 상에서 등고도면(radial 방향), 등위도면(dec-lination 방향), 등경도면(right ascension 방향)으로 나누는 과정이다. 이 때, 등고도면 사이의 간격은 Δr, 등위도면 사이의 간격은 Δδ, 등경도면 사이의 간격은 Δα로 표시하며, 각각 최솟값 rmin, δmin, αmin부터 최댓값 rmax, δmax, αmax까지의 범위의 공간을 나눈다. 이와 같이 공간을 나누면, 네 평면(등위도면, 등경도면)과 두 곡면(등고도면)으로 둘러싸인 셀을 정의할 수 있다. Fig. 4는 이렇게 나누어진 셀의 모습을 나타내고 있으며, 위·아래 방향의 면은 등위도면, 안쪽으로 들어가는 방향과 바깥쪽으로 나오는 방향의 면은 등경도면, 좌·우 곡면은 등고도면이다.
셀마다 고도, 위도, 경도에 따라 인덱스(index)를 부여할 수 있다. 먼저, 등고도면, 등위도면, 등경도면의 기준이 되는 를 다음과 같이 정의한다[10].
여기서, I, J, K는 각각 등고도면, 등위도면, 등경도면에 의해 나뉘는 축별 구간 수이다. 이에 따라, 총 I×J×K개의 cell이 생성된다. 각 셀의 중심 을 다음과 같이 정의한다[10].
여기서, ri, δj, αk는 각 셀의 중심이며, 다음과 같이 정의한다.
이 때, 각 셀의 체적(volume)은 다음과 같이 계산한다[10].
관심대상 영역 및 물체에 따라 셀 정의를 다르게 할 수 있다. Table 1은 MASTER 8의 cell 정의를 나타낸다[11]. 여기서, r = h + RE(RE는 geocentric frame에서의 지구 반지름)이다.
| hmin | hmax | Δh | αmin | αmax | Δα | δmin | δmax | Δδ | |
|---|---|---|---|---|---|---|---|---|---|
| LEO | 186 | 2,286 | 10 | –180 | 180 | 10 | –90 | 90 | 2 |
| MEO | 2,286 | 34,786 | 500 | –180 | 180 | 10 | –90 | 90 | 5 |
| GEO | 34,786 | 36,786 | 20 | –180 | 180 | 10 | –90 | 90 | 2 |
| Unit | km | km | km | deg | deg | deg | deg | deg | deg |
Reprinted from [11].
두 번째 과정에서는 나누어진 각 셀에 대해 충돌 위험 물체가 형성하는 공간 밀도를 계산한다. 충돌을 일으킬 수 있는 물체의 궤도 요소가 알려져 있다고 가정하고, 2체 동역학(2-body dynamics) 모델을 적용하면 해당 물체는 일정한 궤도를 따라 주기적으로 운동한다. 따라서 한 궤도 주기 동안 각 셀에 머무는 시간은 항상 일정하다. 이러한 특성으로 인해, 셀의 경계를 통과하는 '셀 통과 사건(cell passage event)' 정보를 알고 있다면, 한 주기 동안 물체가 각 셀에 머무는 시간을 계산할 수 있다.
에 의해 정의되는 등고도면, 등위도면, 등경도면을 지나는 시기의 진근점 이각(true anomal) 는 다음과 같이 계산할 수 있다[10].
여기서, a, e, inc, ω, Ω는 각각 궤도장반경(semi-major axis), 이심률(eccentricity), 궤도 경사각(inclination), 근점 이각(argument of perigee), 승교점 경도(longitude of the ascending node)이다. 그리고, 는 교점이 존재하는 등고도면, 등위도면의 인덱스 집합으로, 다음과 같이 정의한다.
등고도면과 등위도면은 한 주기에 두 번씩 교차하므로 아래 첨자 1, 2로 각각 표시하였다.
근지점에서부터 특정 진근점 이각 f에 도달하기까지 걸리는 시간은 다음의 식으로부터 계산할 수 있다.
여기서, μ는 지구의 중력상수(gravitational constant)이다. 따라서 충돌 위험 물체 n(총 N개)의 궤도요소를 알고 있다면, 셀(i,j,k)에 진입/이탈하는 진근점 이각 fi,j,k,n,1, fi,j,k,n,2를 Eqs. (9)–(11)을 통해서 계산할 수 있으며, 셀 내 체류 확률 Pi,j,k,n은 다음과 같이 계산할 수 있다.
여기서 Tn는 물체 n의 궤도 주기로, 다음과 같이 계산할 수 있다.
여기서, an은 충돌 위험 물체 n의 궤도 장반경이다. 예를 들어, 물체 1의 궤도 주기가 90분이고 셀(1,1,1)에 머무는 시간이 9분이라면, P1,1,1,1은 0.1이 되어 물체 1이 셀(1,1,1)에 머물 확률이 0.1이라는 의미가 된다. 최종적으로, 모든 관심 물체에 대해 각 셀마다 Pi,j,k,n을 계산하면, 다음의 식을 통해서 각 셀에서의 공간 밀도 Di,j,k를 식 (17)과 같이 계산할 수 있다.
세 번째와 네 번째 과정에서는 앞서 계산된 공간 밀도를 바탕으로 기체 분자 운동론에 바탕을 둔 수식을 활용해 충돌 위험 분석 대상 물체의 평균 충돌 횟수를 산출한다[10]. 충돌 위험 분석 대상 물체가 Δt 동안 N개의 물체와 평균적으로 충돌하는 횟수 c는 다음과 같다.
여기서, vc는 충돌 상대속력, Ac는 대상 물체의 충돌 단면적이고, P′i,j,k는 Eq. (15)를 통해 계산한 충돌 위험 분석 대상 물체의 셀(i,j,k)에서의 체류 확률이다. 실제 각 셀에서의 충돌 상대속력은 다르나, 본 모델에서는 이를 일정 값으로 고정하여 단순화하였다. 또한, 분석 대상 물체와 위험 물체 N개의 궤도 요소에만 의존하는 충돌 플럭스 Fc를 다음과 같이 정의한다.
이때 궤도 요소에 따른 충돌 플럭스를 알면, 대상 물체의 충돌 단면적 Ac, 그리고 시간 구간 Δt에 따라 평균 충돌 횟수를 c = FcAcΔt로도 계산할 수 있다.
충돌 사건이 시간에 무관하게 발생한다고 가정하면 Poisson 과정으로 모델링할 수 있으며, 이에 따라 대상 물체가 Δt 시간 동안 N개의 물체와 m번 충돌할 확률은 다음과 같다[10].
따라서, 대상 물체가 한 번 이상 충돌할 확률은 다음과 같다[10].
3. 개발된 모델과 MASTER-8.0.5의 충돌 분석 결과 비교
본 연구진은 2장에서 서술한 내용을 바탕으로 3차원 셀 모델을 개발하였다. 개발된 모델의 검증을 위해, 모델 산정값과 ESA의 MASTER-8.0.5로부터 얻은 값을 다음 두 가지 결과에 대해 비교하였다. 1) LEO에서의 공간 밀도, 2) 우리별 1·2·3호의 연간 충돌 위험.
개발된 모델의 충돌 위험 분석을 위해서 Space-Track[12]의 데이터베이스에서 획득한 2024년 8월 1일 기준의 TLE 데이터를 사용하였다. 이 중 위성명(satellite name)에 잔해(debris)를 의미하는 ‘DEB’가 포함되지 않은, 즉 잔해가 아닌 위성 및 발사체 상단 등을 포함한 총 14,705개의 물체를 대상으로 하였다. 해당 물체들의 궤도는 SGP4 모델을 이용하여 전파하였으며, 분석 기준 시점은 2024년 8월 1일 00시(UTC)의 상태로 설정하였다. MASTER-8.0.5 분석에서는 최신 데이터인 2024년 8월 데이터를 사용하였다. 이 중 위성 및 발사체 상단 등을 포함하는 발사 및 임무 관련 물체(launch/mission related object)만을 분석 대상으로 하였으며, 이는 두 모델의 충돌 위험 물체 데이터베이스를 최대한 일치시켜 검증하기 위함이다. 또한, 충돌 분석을 위한 셀 정의 파라미터는 Table 2에 나타낸 바와 같이 MASTER-8.0.5와 동일하게 설정하였다.
| Parameter | Value | Unit |
|---|---|---|
| rmin/rmax/ Δr | 400 / 2,000 / 10 | km |
| δmin/δmax/Δδ | –90 / 90 / 2 | deg |
| αmin/αmax/Δα | –180 / 180 / 10 | deg |
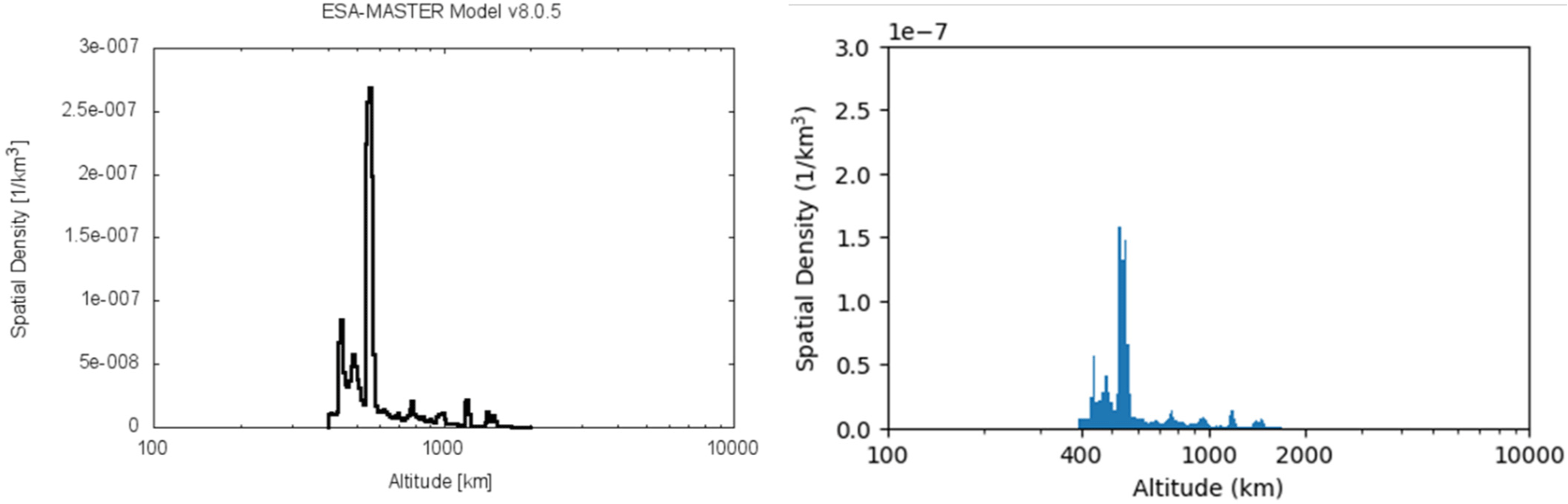
분석 결과를 Fig. 5에 나타냈다. 왼쪽 그래프는 MASTER-8.0.5의 결과, 오른쪽 그래프는 개발된 모델의 결과다. 전반적으로 유사한 값과 경향성을 보이며, 특히 고도 600 km 이상 구간에서는 거의 일치함을 확인할 수 있다. 다만 고도 400–600 km 사이에서는 1–2배 정도 차이가 관찰되는데, 이는 충돌 위험 물체 데이터를 최대한 비슷하게 맞추었음에도 발생할 수밖에 없는 데이터베이스 간 차이에서 기인한 것으로 판단된다. 400–600 km 구간은 Starlink를 비롯한 다양한 우주 임무의 운용 궤도이자 발사 임무의 주차 궤도로도 활용되는 영역으로, 활용하는 데이터베이스에 따라 결과가 달라질 수 있다. 개발된 모델 기반 분석에서는 space-track의 데이터만 단일 소스로 사용한 반면, MASTER-8.0.5는 여러 데이터베이스를 보완적으로 활용하는 것으로 알려져 있다[11].
다음으로 우리별 1·2·3호의 연간 충돌 확률을 계산하였다. 각 위성은 모두 원궤도로 설정하였으며, 충돌 상대속력은 10 km/s로 고정하였다. 계산 결과와 각 위성의 궤도 및 충돌 관련 파라미터는 Table 3에 제시하였다. 연간 충돌 확률은 모두 유사한 수준으로 나타났는데, 이는 세 위성이 MASTER와 개발된 모델의 공간 밀도 계산 값이 거의 일치하는 600 km 이상 고도에 분포하기 때문으로 판단된다.
계산된 확률 값은 10–6–10–8 수준이며, 위성 및 발사체 상단뿐 아니라 파편화된 잔해를 포함할 경우 이 값이 더욱 증가할 것으로 예상된다.
요약하면, 충돌 위험 물체 데이터베이스 차이로 인해 공간 밀도 계산 결과가 특정 고도 구간에서는 1–2배의 차이가 발생하나, 전체적인 수치 수준과 경향성은 양 모델 간에 유사하였다. 또한 우리별 1·2·3호의 연간 충돌 확률 역시 MASTER-8.0.5와 개발된 모델 모두에서 비슷한 수준으로 평가되어, 본 연구의 3차원 셀 모델이 이론적 기반 위에서 충실히 구현되었음을 확인할 수 있다.
4. 결론
우주 공간의 접근성이 높아지고 그 가치가 증대함에 따라, 우주 공간은 인류 개발 이래 가장높은 혼잡도를 보이고 있으며 앞으로도 더욱 심화될 전망이다. 따라서 우주자산의 안전한 운영과 우주 공간의 지속가능한 이용을 위해서는 우주물체 환경에 대한 정확한 이해와 분석을 통해 다양한 의사결정을 지원할 수 있어야 한다.
이를 위해 본 연구에서는 우주자산 충돌 위험 산정을 위해 유연한 확장이 가능한 3차원 셀 모델의 이론적 기반을 정립하고, 이를 바탕으로 소프트웨어 구현을 완료하였다. 개발된 모델의 타당성을 검증하기 위해 ESA의 MASTER-8.0.5와 유사한 조건 하에서 공간 밀도 및 충돌 위험 분석을 수행하였으며, 두 모델이 유사한 수준에서 충돌 위험을 평가함을 확인하였다.
향후 개선된 우주물체 데이터베이스와 결합될 경우, 본 연구의 3차원 셀 모델이 높은 충실도(fidelity)를 가지는 충돌 위험 분석 결과를 제공할 것으로 기대된다. 또한 해당 모델을 활용해 우리나라 우주자산의 다양한 운용 시나리오별 충돌 위험을 심층 분석함으로써 안전하고 효율적인 운용 전략 및 정책 수립에 기여할 수 있을 것이다.