1. 서론
여행 계획을 만든다고 상상해 보자. 가장 먼저 해야 할 일은 무엇이고, 그 밖에 어떤 준비들이 필요할까? 제일 먼저 떠오르는 것은 아마 목적지를 정하는 일일 것이다. 또는 언제 출발해서 언제 돌아올지, 출발일과 도착일부터 결정해야 할 것이다. 대체로 여행 계획은 이 두가지 질문에 답하는 것으로 시작할 것이다. 그 외에 생각해 볼 수 있는 질문은 다음과 같을 것인데, 이러한 질문들은 결국 행성탐사임무의 설계 과정을 시작하기 위한 질문들과 유사해 보인다.
-
여행지까지 오고 가는 교통편 → 발사체와 우주선(launch vehicle and spacecraft)
-
여행지에서 할 일 → 임무 유형(mission type: flyby/rendezvous/sample return)
-
가지고 갈 것 → 임무 탑재체(mission payloads)
-
여행 비용 → 탐사선 개발 및 발사, 운영에 필요한 소요비용
-
연락 방법 → 통신 및 운영 수단(communication and operation)
-
부수적인 일정들 → 기타 임무(miscellaneous missions)
-
여행의 기록과 정보 공유 → 자료처리와 배포(data processing and distribution)
이와 같은 관점에서, 본 논문에서 논하고자 하는 것은 여행의 적절한 시기, 즉 행성탐사 임무를 수행하기 위한 적절한 시기를 탐색하는 방안에 대한 기본적인 방법에 대해 논하고자 한다.
또한, 한국형 발사체(KSLV, Korea Space Launch Vehicle-II) 누리호의 개발이 완료되면 미래에는 우리나라의 발사체와 초소형 위성(CubeSat)을 이용하여 지구접근 소행성들을 직접 탐사하는 임무도 가능할 것으로 예상된다. 이에 본 논문에서는 지구에 접근하는 소행성을 대상으로 향후 우리나라에서 탐사 임무를 실행할 때를 대비하여 일반적인 행성탐사선의 임무 수행시기를 결정하는 방법에 대해 설명하고자 한다.
앞서 질문으로 돌아가서, 여행의 시기를 결정하는 기준은 목적지를 결정하는 것과 다시 연관되어질 수 있다. 즉, 여행 목적지의 특징에 따라 적합한 방문 시기도 달라질 수 있는 것처럼, 마찬가지로 행성탐사 임무에서도 목적지 행성에서 특별한 이벤트가 있다거나, 지구와의 근접 시기가 달라진다거나 하는 조건에 따라 발사 시기를 조절해야 하는 상황이 생길 수 있다. 이처럼 행성탐사 임무의 수행시기를 결정하기 위해서는 여러 차례의 해석 과정이 반복되어야 하므로 이를 위한 설계해석 소프트웨어 도구가 준비되어야 한다. 또한 그러한 반복과정을 사전에 염두에 두고, 해석과 설계 과정을 진행해야 할 것이다.
2. 지구-화성간 탐사선 발사시기 탐색
지구 중력권을 벗어나 태양계의 다른 행성들, 즉 화성이나 목성, 토성, 소행성탐사 임무를 설계하기 위해서 가장 먼저 해야 할 일은 탐사선 발사가 예상되는 기간 중, 각 연도별로 탐사선의 전이궤도 투입에 소요되는 에너지를 산출하는 일이다. 1960년대 초부터 금성과 화성으로 행성간 탐사선을 보냈던 미국 NASA에서는 이러한 전이궤도 투입 에너지 산출을 위해 여러가지 프로그램을 개발하여 사용하고 있고, 그 중에 대표적인 것인 JPL(Jet Propulsion Labo-ratory)에서 개발한 MIDAS(Mission Design and Analysis Software for the optimization of ballistic interplanetary trajectories) 프로그램이다. 대외비 프로그램인 MIDAS를 사용해서 NASA에서는 금성, 화성, 목성, 토성 등 주요 행성으로의 연도별 전이궤도 투입 에너지를 계산한 보고서를 정기적으로 발간하고 있으며, 이는 NASA에서 중장기 행성탐사 임무계획을 수립할 때 기초 자료로 사용된다[1,2].
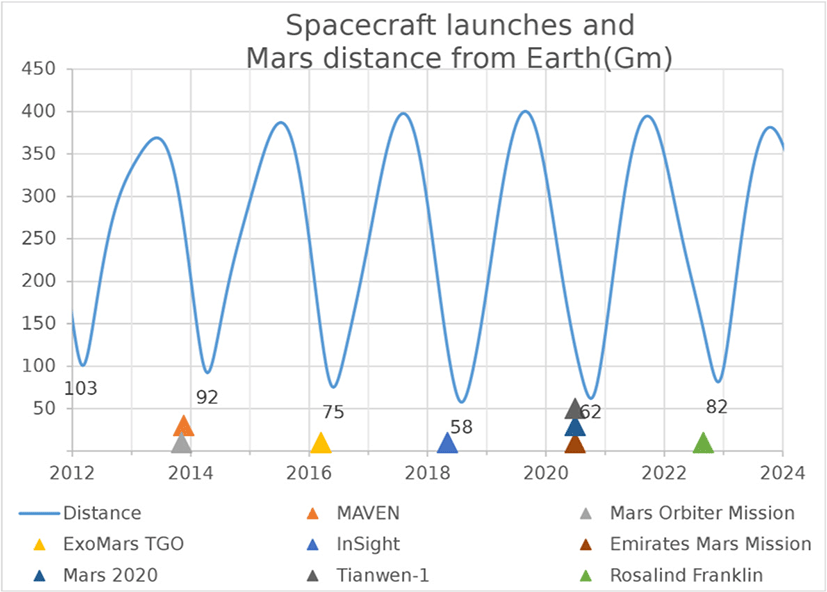
Fig. 1은 근래에 발사되었거나 발사 준비 중인 화성탐사선들의 발사 계획을 나타내고 있다[3]. 이 그림에서 알 수 있듯이 지구에서 화성으로 향하는 탐사선의 발사 기회는 대략 두 행성의 회합주기인 2년마다 찾아온다. 각 회합주기마다 최대, 최소 거리가 동일하지 않은 이유는 두 행성의 궤도가 완전한 원이 아니며, 공전궤도면 역시 동일 평면에 있지 않기 때문이다. Fig. 1을 보면 대부분의 화성 탐사선 발사는 화성과 지구 사이 거리가 가까워지는 시기에 진행된 것을 알 수 있다.
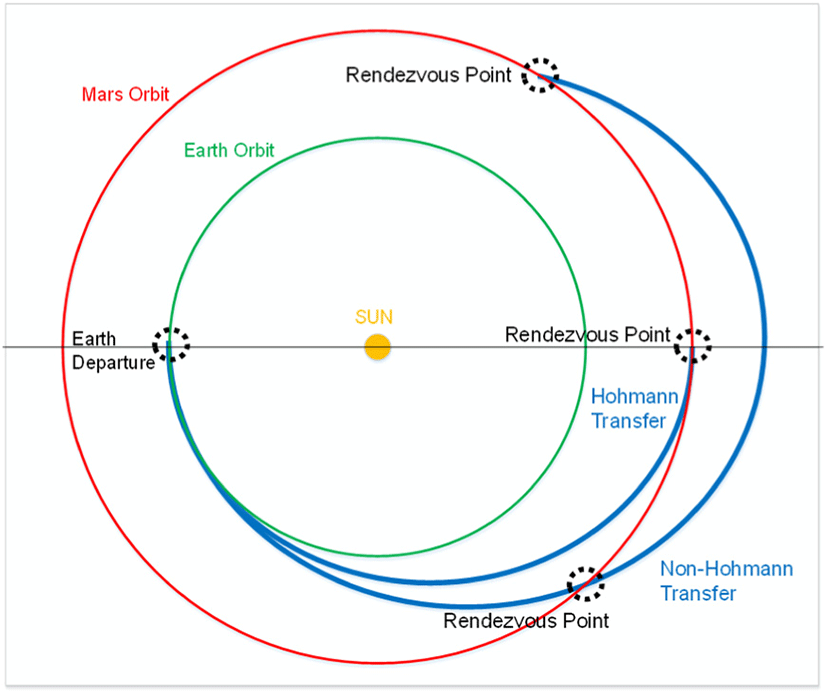
행성간 전이궤도 선정을 위해서는 먼저 출발지 행성과 도착지 행성의 천체력 입력이 필요하다. 여기서는 출발지 행성은 지구, 도착지 행성은 화성으로 가정하였다. Fig. 2는 지구-화성 간에 형성될 수 있는 여러 형태의 비행경로를 보여준다. 만약, 비행기간과 소요 에너지의 제한이 없다면 그림에서 보는 것처럼, 이론적으로 가능한 전이경로의 숫자는 무한개가 되고, 출발지점이 반드시 근일점이어야 할 이유도 없어질 것이다.
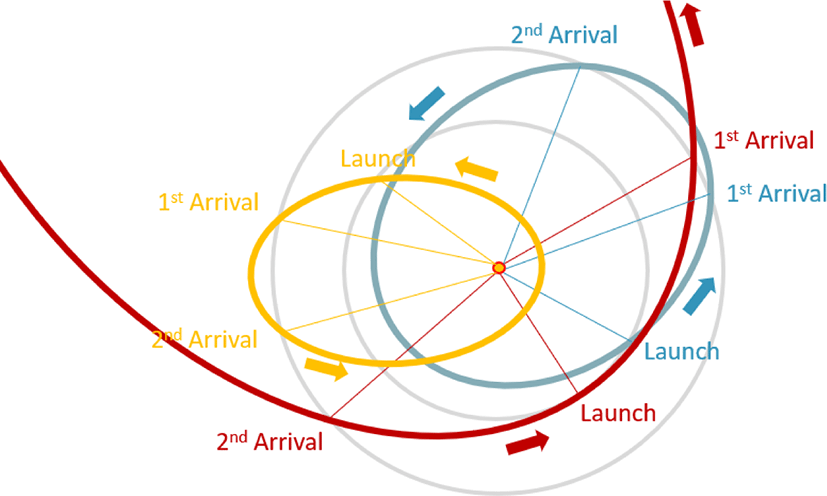
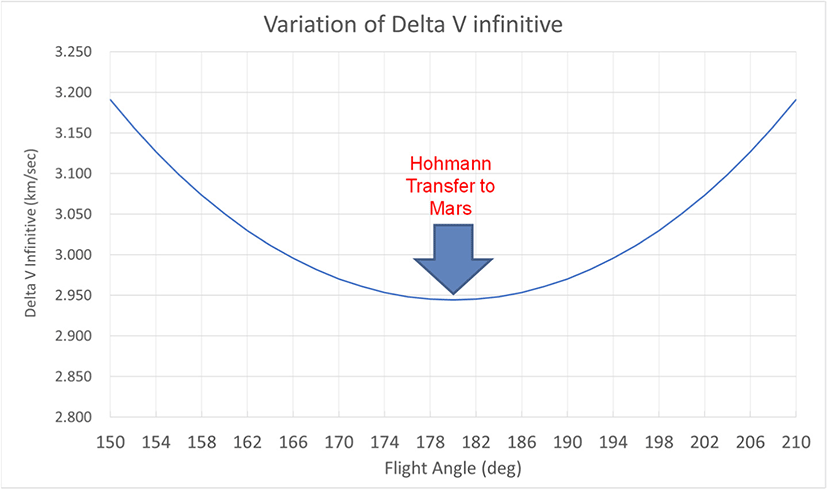
Fig. 3에는 지구 중력권을 벗어나 화성궤도에 도달하기 위한 최소 에너지 경로, 즉 호만 궤도전이(Hohmann transfer, 비행각=180도)에서의 소요에너지를 구하기 위한 도표를 나타내었다. 해당 그래프를 참고하면, 호만 궤도전이 경로를 따라 지구 중력권을 탈출하여 화성 궤도까지 가기 위해서는, 지구의 공전궤도 속도(약 29.87 km/sec)에 더해서 지구중력권 경계에서 약 2.94 km/sec의 추가 속도가 필요한 것으로 예상된다[4–6].
우리나라 기술로 개발한 누리호 발사체(KSLV-II)로 지구중력권 탈출을 시도하는 경우의 예상 성능을 시뮬레이션해 보았다. KSLV-II 전체 중량 및 3단 엔진 중량 및 연소시간 등의 정보를 Wikipedia 공개자료 및 KISTEP 예비타당성조사 보고서 요약본에서 참고하여 지구중력권 탈출 속도 및 화성 전이궤도에 탐사선을 투입할 수 있는 최소의 가능한 중량을 개략적으로 예측해본 내용을 Table 1에 보였다[7,8].
3. 람베르트 문제의 해 구하기(Lambert Problem’s Solution)
탐사대상이 결정되었다는 전제 하에, 지구 중력권을 벗어나는 행성간 임무설계 과정의 첫 단계는 최적의 발사기회, 즉 최소의 에너지로 목적지 행성과 랑데부(rendezvous)할 수 있는 시기가 언제인지를 계산하는 것이다. 지구를 출발해서 행성으로 향하거나, 행성을 출발해서 지구로 돌아오는 최적의 발사 시기 산출을 위해서는 출발일자와 도착일자를 경계 조건으로 하는 람베르트 문제(Lambert’s problem)의 해를 구하는 과정이 필요하다. 람베르트 문제의 해를 구하는 알고리즘은 여러 사람에 의해 연구되었고, 각각의 장단점이 존재한다[9–12].
본 절에서는 연도별로 지구에서 화성으로의 비행경로에 탐사선을 투입하는데 필요한 에너지량을 산출하는 프로그램을 작성하였고, 이를 이용해서 2026–2045년 기간 동안 연도별 지구-화성간 탐사선의 전이궤도 투입 에너지량을 비교하였다. 계산에 필요한 행성들의 천체력으로 JPL의 DE431 파일을 사용하였고 람베르트 문제의 해를 구하기 위해 배틴-보간(Battin-Vaughan‘s)의 Elegant Lambert 알고리즘을 적용하였다[13,14]. 계산된 결과를 2010년에 NASA에서 발행한 행성간 임무설계 핸드북(interplanetary mission design handbook)의 동일기간 화성탐사임무 발사 소요 에너지와 비교하였다[15].
지구-화성 간의 랑데부(rendezvous)가 성립하기 위해서는 행성간 비행이 종료되는 시점에 탐사선이 도착한 궤도상 지점에 목적지 행성이 존재해야 한다. 이를 계산하기 위해서는 람베르트 정리(Lambert’s Theorem)로 알려진 다음 정리를 이용한다.
“원추곡선(Conic Trajectory) 상에서 두 지점 간의 비행시간은 다음 세 가지 변수에 의해 결정된다.”
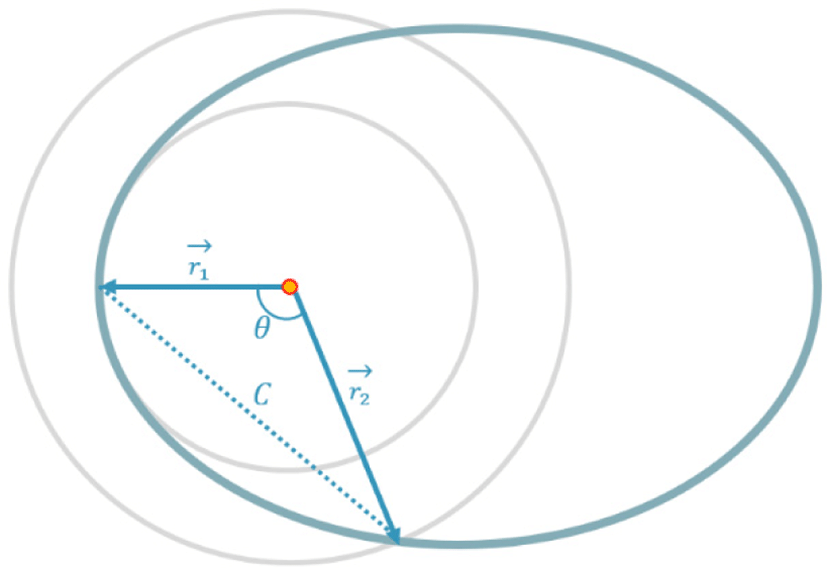
위에서 첫 번째와 두 번째 변수는 두 행성의 궤도 방정식이나 천체력, 즉 JPL에서 계산한 DE431과 같은 수치자료에 의해 구할 수 있다[16]. 첫 번째와 두 번째 변수는 거의 상수와 같아서 소요 에너지 변화에 큰 영향을 주지 않는다. 결국 세 번째 변수인 궤도 장반경의 변화에 따라 전이궤도의 전체 형상이 결정되며, 이에 따라 소요 에너지가 결정된다. 람베르트 정리를 그림으로 나타내면 Fig. 4와 같다. 여기에서 출발지 행성과 도착지 행성 간의 직선거리와 두 행성의 궤도 반경 사이에는 다음과 같은 관계가 성립한다.
두 행성 간의 궤도전이 시에 호만궤도(Hohmann orbit)을 따르면 최소 에너지가 소요된다는 원리는 잘 알려져 있다[17]. 다시 말해서, 행성 간의 모든 궤도전이 경로에 소요되는 에너지는 호만궤도에서의 에너지보다 반드시 크다는 의미이다. 그래서 행성 간 전이궤도를 찾을 때에는 검색을 원하는 출발일과 도착일에 해당하는 호만궤도(비행각 = 180도)를 먼저 구한 다음, 궤도장반경을 조금씩 늘려가면서 랑데부가 가능한 경로를 찾는 것이 탐색 알고리즘의 기본 원리이다. 이때, 비행 경로의 비행각이 180도 미만이면 제Ⅰ형(Type Ⅰ), 180도 이상이면 제Ⅱ형(Type Ⅱ)으로 각각 분류한다(Fig. 5)[18,19].
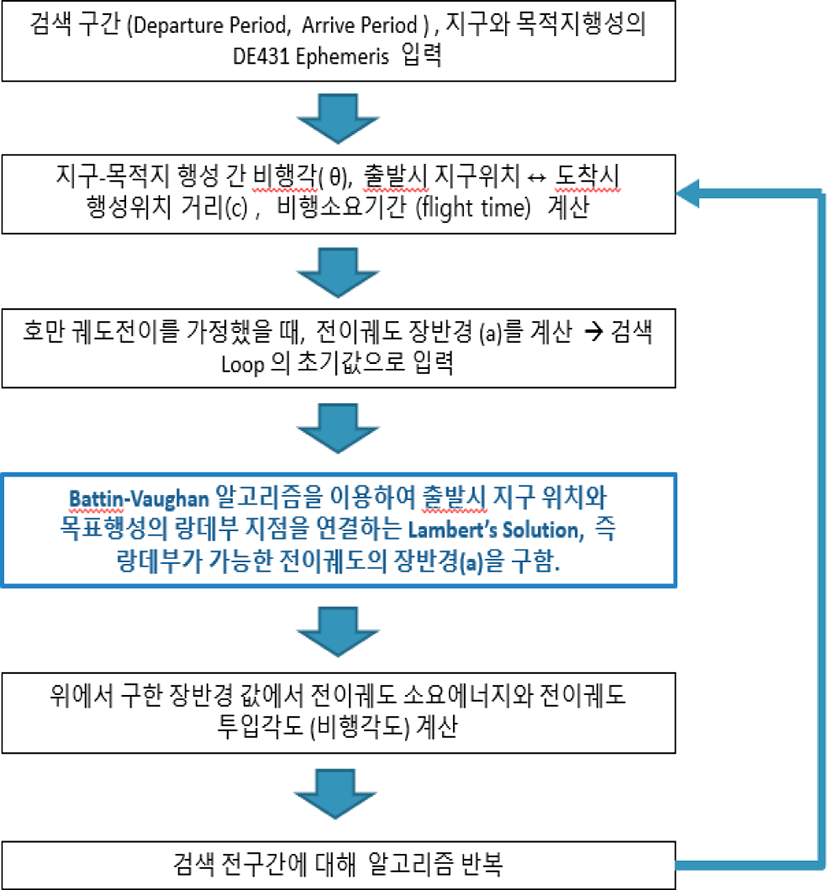
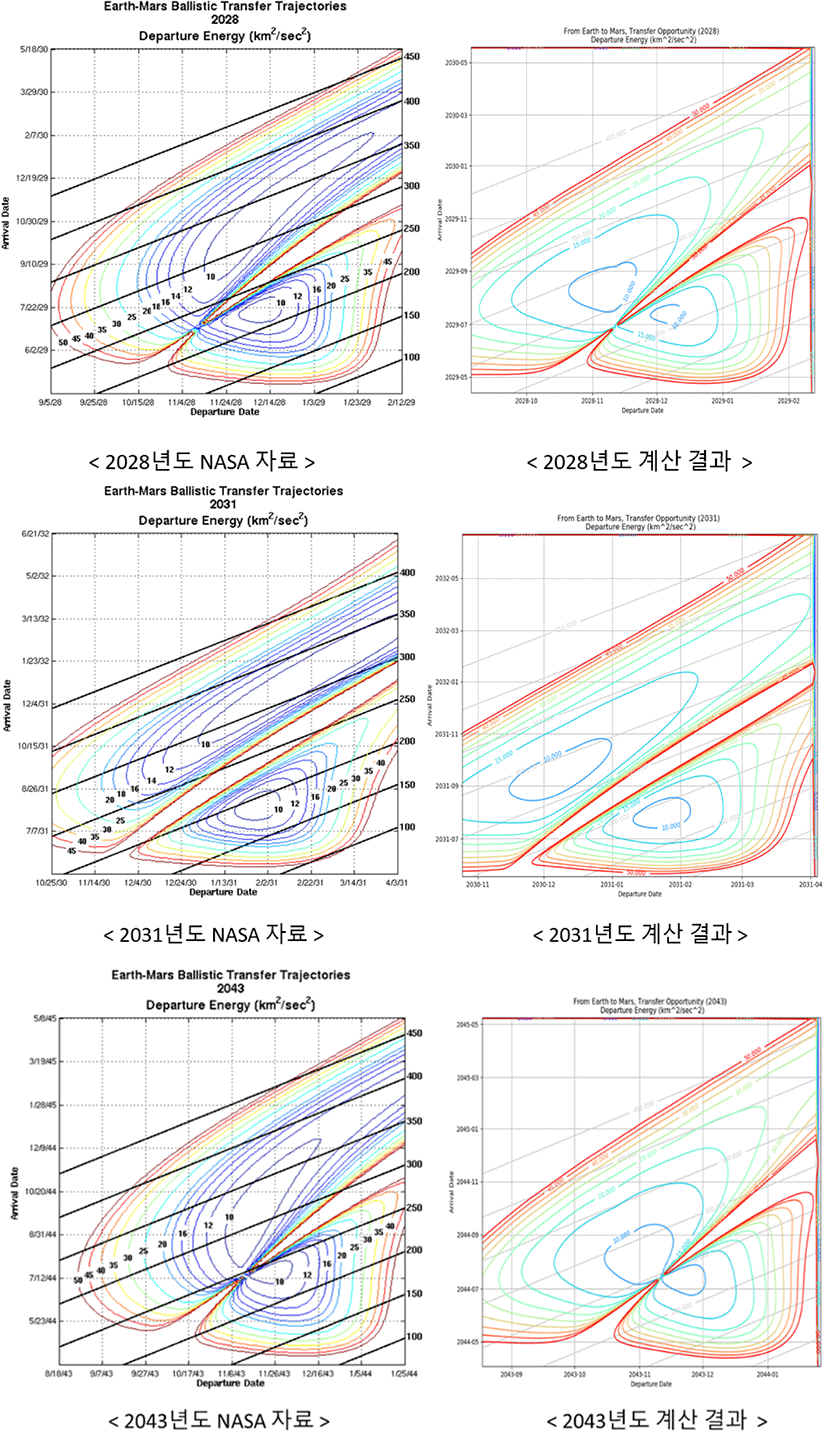
람베르트 문제의 해를 구하기 위한 알고리즘으로 본 연구에서는 배틴-보간(Battin-Vaughan’s)의 Elegant Lambert 알고리즘을 적용하였다. 행성간 전이궤도 투입 에너지 산출 알고리즘을 요약하여 흐름도로 나타내면 Fig. 6과 같다. 이러한 알고리즘에 의하여 개발한 프로그램으로 2026–2045년 기간 동안의 지구-화성간 전이궤도 투입 에너지량을 나타내는 Pork-chop 도표를 작성하였으며 몇 개의 예를 Fig. 7에 나타냈다. 각 결과, 그림을 NASA의 MIDAS에 의해 작성된 동일 연도의 Pork-chop 도표와 비교하였다.
4. 지구접근 소행성 탐사선의 발사시기 산출
2000년대에 들어서 지구접근 소행성의 연구자료를 얻기 위한 우주탐사 임무가 활발히 진행되고 있다. 이러한 임무에는 기존의 중소형 크기의 탐사선뿐만 아니라, 초소형위성(CubeSat) 또는 큐브크래프트(CubeCraft)로 불리는 소형 탐사선들을 투입하는 방법도 제안되고 있다[20]. Table 2에는 최근에 진행 중인, 해외의 대표적인 소행성 탐사선 프로그램을 나타내었다. 또한 이 탐사선들이 목적지로 삼은 주요 소행성들의 궤도를 Fig. 8에 나타내었다.

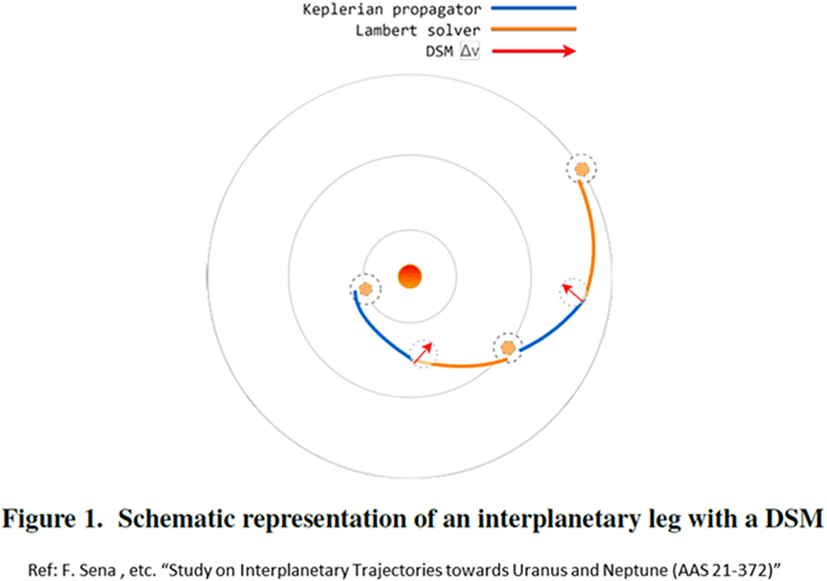
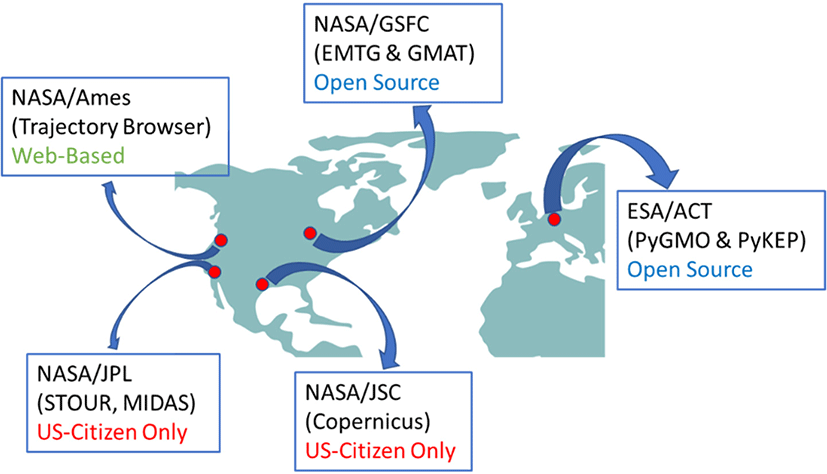
근래에 지구 접근 소행성을 비롯해서 행성간 탐사선 경로를 설계할 때에는 “Interplanetary Leg” 개념을 도입하여 사용한다(Fig. 9)[21,22]. 이것은 행성간 탐사선의 전체 비행경로를 몇 개의 단위로 나누는 것인데, 지구를 떠난 중력 보조기동을 위해 여러 번의 행성 접근 비행을 할 때, 각 행성과 행성 사이의 비행 단위를 “Interplanetary Leg”로 정의한다. 예를 들어, 지구에서 목성을 가기 위해 지구(출발)-금성(중력보조기동)-지구(중력보조기동)-화성(중력보조기동)-목성(도착)을 했다면 그 경로는 ‘E-V-E-M-J’이고, 4개의 interplanetary leg으로 구성되는 셈이다. 각 leg에는 출발 지점과 도착 지점을 정의하여 이를 연결하는 경로를 먼저 구한다. 그리고 람베르트 해 구하기(Lambert’s solver) 알고리즘으로 해당 경로를 구현하는데 필요한 출발 속도와 도착 속도를 구하게 된다[23]. 또한 필요에 따라 DSM(deep space maneuver)과 GAM (gravity assist maneuver)을 조합한 leg를 만들 수 있다. 이러한 개념을 활용해서 필요한 수만큼의 여러 개의 leg를 마치 레고 블록처럼 조합하면 이론 상으로는 무한개의 행성간 경로가 만들어진다. 여기에 출발일과 도착일, 최대 가능 추력, 가능한 탐사선의 질량 등의 제약조건(constraints)를 도입하여 실현이 불가능한 경로들을 후보에서 제외하고 최적의 경로 만을 구하는 알고리즘을 사용한다[24]. 이러한 방법을 적용하는 경로설계 소프트웨어가 근래에 많이 연구가 되고 있는데, 그 대표적인 기관과 프로그램 이름을 Fig. 10에 보였다. 이러한 전역 경로 최적화(Global Trajectory Optimization) 프로그램은 대부분 In-House 코드(자체 개발한 비공개 프로그램)로 사용되지만 제한적으로 공개하거나 완전 오픈소스로 사용할 수 있도록 공개한 프로그램도 있다. 그 중에 대표적인 프로그램이 NASA/GSFC(Goddard Space Flight Center)의 EMTG(Evolutionary Mission Trajectory Generator)와 ESA/ACT(Advanced Concept Team)에서 개발한 PyGMO/PyKEP 프로그램이다[25–31]. 이러한 오픈소스 프로그램들은 저추력(low-thrust) 엔진을 사용한 탐사선의 경로설계에도 적절하게 활용되고 있다[32,33]. Fig. 11에 보인 것처럼, NASA/Ames Research Center에서는 인터넷 상에서, 행성탐사선의 비행시기와 경로를 실시간으로 산출하여 제공하는 웹서비스를 운영하고 있다. 그리고 EMTG 프로그램은 오픈 소스이긴 하지만 이를 실행하기 위해서는 스탠포드대학교에서 개발한 유료 프로그램인 SNOPT 최적화 라이브러리가 필요하다[34].
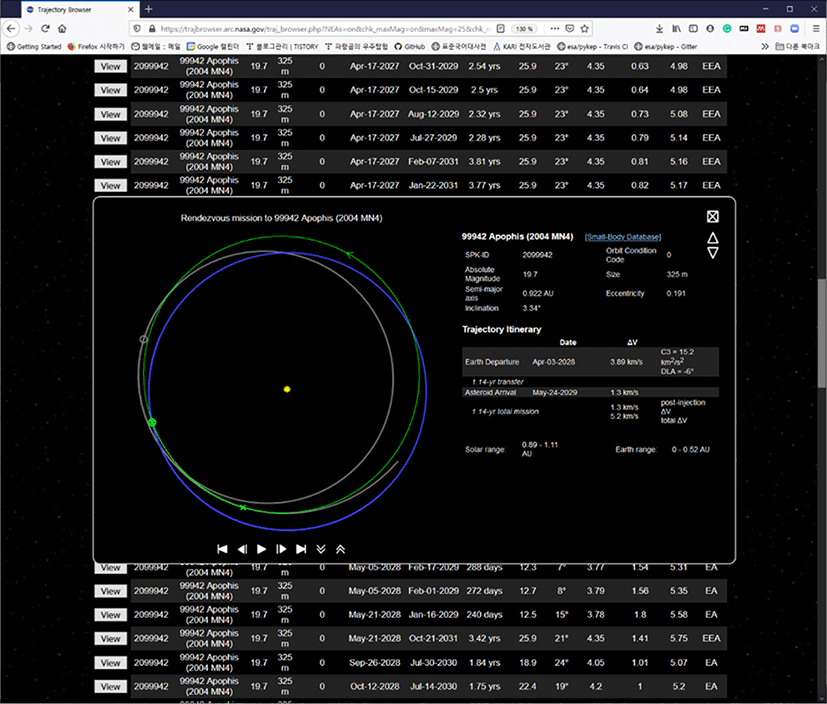
본 절에서는 공개 소프트웨어를 사용하여 소행성 탐사선의 발사 시기와 비행 경로의 후보를 산출하는 방법을 보이기 위해, EMTG(NASA/GSFC 개발)를 이용하여 소행성 아포피스(Apophis)로 향하는 탐사선의 경로를 탐색해 보았다.
아포피스 소행성은 2004년 6월에 처음 발견된 대표적인 지구접근 소행성으로서, 2029년 4월에 정지궤도위성의 궤도보다 안쪽으로 지구에 근접할 것으로 예상되는 천체이다[35]. 아직까지 근접 비행한 탐사선이 없었고, 지구상의 천체망원경으로는 배율의 한계가 있어서 정확한 형상은 알려지지 않았으며, 대략의 궤도 운동 특성만 알려져 있다(Fig. 12). Table 3에는 현재까지 알려진 아포피스 소행성에 관한 요약된 정보들을 나타내었다.
| Mission target | 99942 apophis |
|---|---|
| 발견시기, 발견자 | 2004년 6월, Tucker RA, Tholen DJ, Bernardi F |
| 평균 궤도속도 | 30.78 km/sec(지구 29.78 km/sec) |
| 추정크기 | 370 meters |
| 공전주기 | 0.89 year |
| 특이사항 | 2029년 4월 13일, 지구근처 36,000 km 접근 예상 |
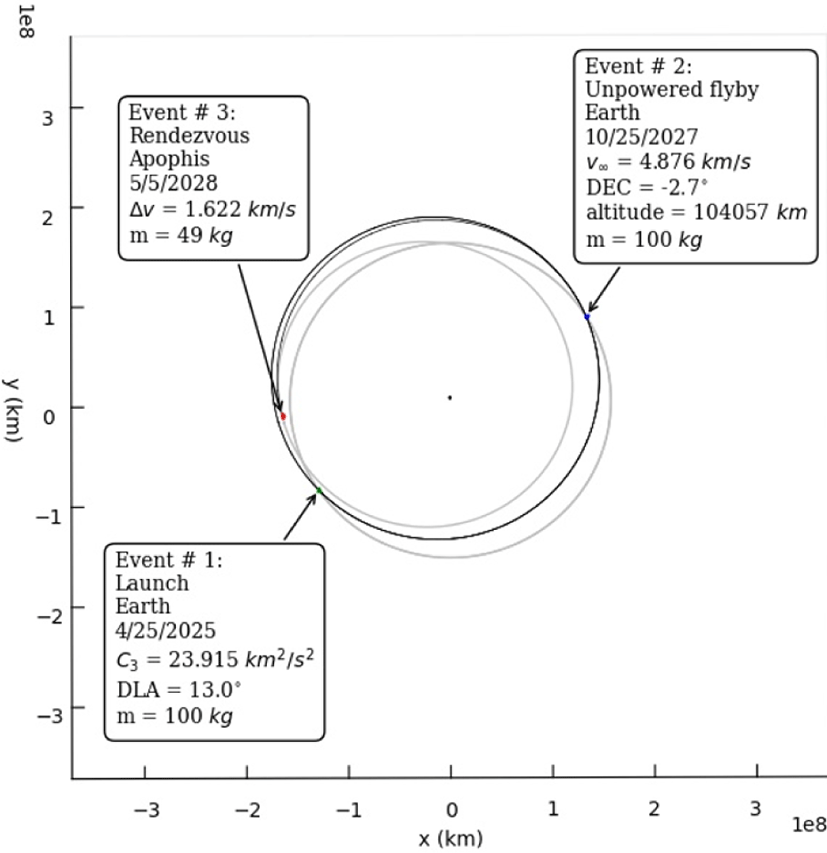
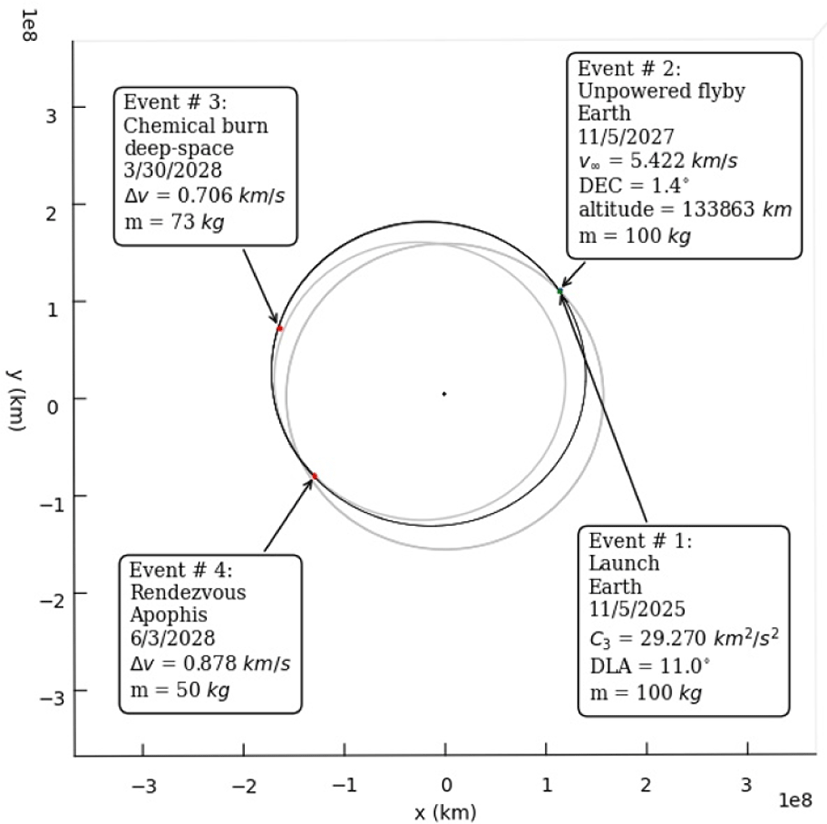
Fig. 13과 14에는, 지구에서 출발하여 DSM을 수행하지 않는 경우와 1회 수행하고 아포피스 소행성과 랑데부를 하는 비행 경로의 예를 각각 보였다. 여기서 지구 중력권 탈출 시의 탐사선 질량은 100 kg으로 가정하였다. 앞서, interplanetary leg 계산 원리에 설명하였듯이, 여기서도 필요에 따라 DSM과 GAM의 횟수 입력 파라미터를 조절하여 반복 계산함으로써 여러가지 경우의 가능한 비행 경로를 만들어낼 수 있다. 그 다음으로, 임무와 경로 설계 목적(최소 비행시간 또는 최소 에너지 등), 그리고 가용한 발사체의 발사 능력에 적합한 경로를 선택하는 것이 가능하다.
5. 결론
이상과 같이 본 논문에서는 향후 우리나라에서 추진하는 소행성 탐사임무를 대비하여 적합한 발사 시기를 산출하기 위한 기본적인 방법에 대하여 서술하였다. 적절한 발사시기 산출을 위해서는 첫째, 지구를 비롯한 태양계 행성들과 목적지 소행성의 정확한 천체력을 확보해야 하며, 둘째, 일련의 비행계획이 준비되어야 한다. 이 비행 계획은 일종의 임무 시나리오로서, 발사체의 성능 정보, 중력보조기동(gravity assist maneuver)의 횟수, DSM의 횟수, 탐사선의 주엔진 특성 등의 정보를 의미한다. 끝으로 경로 설계와 해석, 최적화를 위한 임무해석 및 설계 프로그램을 갖추어야 한다.
일반적으로 소행성 탐사의 시작부터 임무 종료까지는 장구한 시일이 소요되므로 다양한 환경 변화(예산, 기술 문제, 부품 수급, 설계 변경, 발사 일정 변경 등등 …)를 대비하여 융통성 있는 계획을 만들어야 한다. 특히, 소행성 탐사선 발사 시기는 여러 가지 요인에 의해 변경될 수 있어서 임무 경로의 해석과 설계의 시작 단계부터 지루한 반복과 빈번한 재설계 과정을 거쳐야 함을 염두에 두어야 한다. 여러가지 상황 변동으로 인해 발사일자가 바뀔 경우, 그에 따른 발사체의 발사각 변경과 시간 변경, 새로운 비행 시나리오를 사전에 준비하거나 실시간으로 계산할 수 있어야 한다. 이러한 이유에서 경로설계 및 해석 프로그램은 필수불가결한 요소에 해당한다.
단, 경로 설계 및 해석 프로그램은 수치적인 계산 결과만을 내어 놓을 뿐, 실제로 비행할 하드웨어(탐사선과 발사체)의 성능, 지상국과의 통신가용도(contact visibility) 등에 따라 실행이 가능한지를 최종적으로 판단하는 것은 탐사선 운영자의 경험과 판단에 의한다.
경로설계와 해석 프로그램은 1) 자체 개발하거나, 2) 상용 프로그램 구입, 그리고 3) 오픈 소스를 활용하는 방법 중에서 선택할 수 있을 것이다. 각 방법에 따라 장, 단점이 있는데, 특히 본 논문에서 사용한 오픈 소스 프로그램을 활용할 경우에는 개발에 필요한 비용과 시간을 크게 단축할 수는 있으나 프로그램 구조와 사용법에 대한 상세한 설명이 제공되지 않아 사용자는 스스로 시간과 노력을 들여 내용을 이해하여야 적절한 활용이 가능하다.