1. 서론
Celestak의 SATCAT(SATellite CATalog)에 따르면 현재까지 궤도상에 발사된 이후 지구 대기로 재진입하거나 무덤궤도 등으로 천이된 물체의 수는 25,500여 개이며, 이 중 대부분은 지구 대기로 재진입하는 저궤도 물체이다[1]. 크기가 작은 물체들은 대기로 재진입하면서 분해되거나 소각되지만 2,000 kg 이상의 대형물체의 경우 10%–40%가 생존하여 지상으로 낙하하고 있다[2]. 현재까지 대부분의 재진입 물체는 해상에 낙하하여 피해를 야기하지 않고 있으나, 코스모스 954(1978), 스카이랩(1979), 델타2 발사체(1993), 델타2 발사체 연료탱크(1996), 스페이스셔틀(2003) 등 실제 지상에 낙하한 사례도 분명히 존재한다[3–11]. 통계적으로 제어되지 않은 2,000 kg 이상의 물체는 1주일에 1개씩 재진입하고 있다.
이와 같은 상황에서 국제우주쓰레기조정위원회(IADC, Inter-Agency Space Debris Coor-dination Committee)는 1997년 우주물체 재진입 관측데이터 및 분석데이터 공유 방안을 채택하였고, 1998년부터 유럽우주국 주관으로 재진입 시점 예측 캠페인을 매년 1–2회 수행하고 있다. 해당 캠페인은 IADC 회원기관들이 잠재적 위험 물체를 선정하고, 재진입 시점 예측을 위한 분석 툴이나 절차를 시험하는 것이 주요 목적이며, 한국항공우주연구원은 IADC의 회원기관으로 2015년부터 본 캠페인에 참여하고 있다.
재진입 예측은 궤도의 불확실성, 대기밀도의 불확실성, 재진입 대상의 자세 및 단면적, 무게 등 정확한 정보의 부재 등으로 정밀한 분석이 어렵다. 이를 보완하기 위한 연구들이 지금까지 활발하게 진행되고 있다. Anilkumar는 다수의 TLE(Two Line Element) 데이터를 이용하여 궤도정보를 산출하고, 칼만필터를 적용하여 재진입 예측을 수행하였다[12]. Pardini는 재진입 분석에 다양한 대기밀도 모델을 적용하여 대기밀도 모델의 민감도를 분석하였고, 다수 IADC 캠페인에서 가장 잘 맞는 대기밀도 모델을 도출하는 연구를 수행하였다[13,14]. Yurasov는 대기밀도 계수의 조정을 통해 재진입 분석 정확도를 높이는 연구를 수행하였고, 100개 이상의 많은 TLE 데이터를 이용하여 대기밀도 계수를 조정한 후 궤도결정 및 예측을 수행하였고, 기존 대비 성능 향상을 확인하였다[15]. 그 외에 Dodin[16]은 이론적 탄도계수의 한계점 연구, Reyhanoglu[17]는 재진입 물체의 분열 시 파편의 낙하 분포, Pardini[18]는 USA-193는 재진입 예측 연구 등을 각각 수행한 바 있다.
위와 같이 비제어 재진입 물체의 재진입 예측을 위해 다양한 연구들이 수행되었고, 지속적으로 예측 정밀도를 향상시키기 위한 연구들이 수행되고 있으나 초기궤도 및 대기밀도의 불확실성, 재진입 물체의 정확한 자세 및 단면적, 무게 정보의 부재 등의 원인으로 여전히 정확한 재진입 시점을 예측하는 것은 매우 도전적인 분야이다. 이에 본 연구에서는 IADC 재진입 캠페인의 분석 정확도 향상을 위해 다수의 TLE 데이터를 이용한 탄도계수 최적화 기법을 제안하였다. 탄도계수를 최적화하는 방법은 종전에 제안되지 않았던 방식으로 물체의 물리제원이나 자세정보 등의 불확실 요소가 존재하는 상황에서 다수의 TLE 데이터를 활용한 장반경 변화를 가장 잘 추종하는 탄도계수를 탐색하는 방법으로 재진입 예측 정밀도 향상에 기여할 수 있을 것으로 판단된다. 제안한 기법을 2021년도 2차 IADC 재진입 캠페인의 대상인 창정 5B 발사체에 적용하여 재진입 시점을 예측하고, 실제 재진입 시점과 차이와 캠페인 참여 기관들의 평균오차와 비교 분석하였다.
2. 방법론
재진입 캠페인의 타깃은 저궤도 영역에서도 낮은 고도의 물체이며, 지상에 피해를 줄 수 있는 큰 규모의 물체들이 선정된다. 따라서 대기저항이 물체의 궤도에 미치는 영향이 상대적으로 높아짐을 의미하고, 정밀하게 모델링된 지구 비대칭 중력장에 비해 불확실성이 높은 대기저항의 영향을 잘 예측하는 것이 재진입 시점 예측의 핵심이라고 할 수 있다.
구체적인 결과는 타깃이 고도 80 km에 도달하는 시간을 의미하는 재진입 시점(re-entry time)이며, 지상표면의 낙하지점이나 충돌시간을 의미하는 것은 아니다. 일반적으로 고도 80 km 인근에서 재진입 물체의 분열이 이루어져 내부 부품들이 흩뿌려지게 되고, 고도 80 km 도달 지점으로부터 진행방향으로 수천 km의 분포범위를 가지기 때문에 정확한 위치나 시간을 정의하기 어렵기 때문이다.
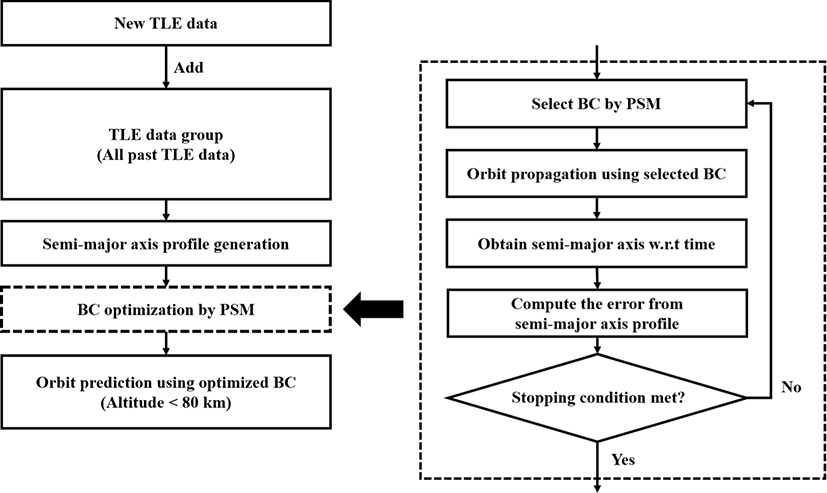
이에 본 연구에서는 최적화 알고리즘을 적용하여 탄도계수를 추정하고 이를 이용하여 재진입 시점예측을 수행하는 전략을 적용하였다. 해당 전략은 크게 기준 장반경 프로파일 생성, 탄도계수 최적화, 정밀궤도전파의 3가지 단계로 나눌 수 있다.
첫 번째, 기준 장반경 프로파일 생성에서는 현재까지 획득한 재진입 물체의 모든 TLE 데이터에서 각각의 기산일에 해당하는 위치를 추출하고, 이를 접촉궤도(osculating orbit) 형태로 바꾸어 장반경 정보를 획득한다. 결과적으로 TLE 데이터의 숫자만큼 장반경 프로파일을 구성하는 장반경 정보가 생성된다.
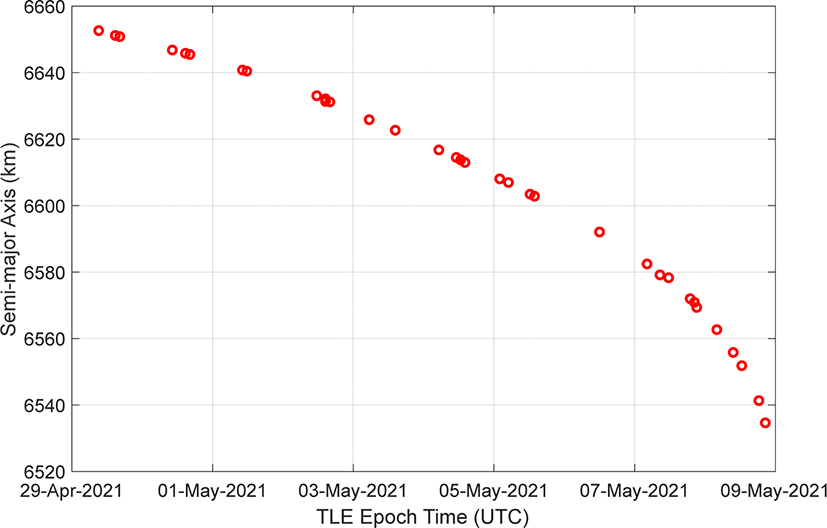
Fig. 1은 장정 5B호 발사체의 장반경 프로파일을 나타낸다. TLE 데이터가 갱신됨에 따라 장반경이 점차 낮아지며, 재진입 시점에 가까워질수록 급격하게 고도가 낮아짐을 확인할 수 있다.
다음 단계는 생성된 장반경 프로파일과 가장 잘 맞는 탄도계수를 찾는 것이다. 통상적으로 탄도계수(BC, Ballistic Coefficient)는 항력계수(Cd), 질량(M), 단면적(A)의 함수로 구성된다.
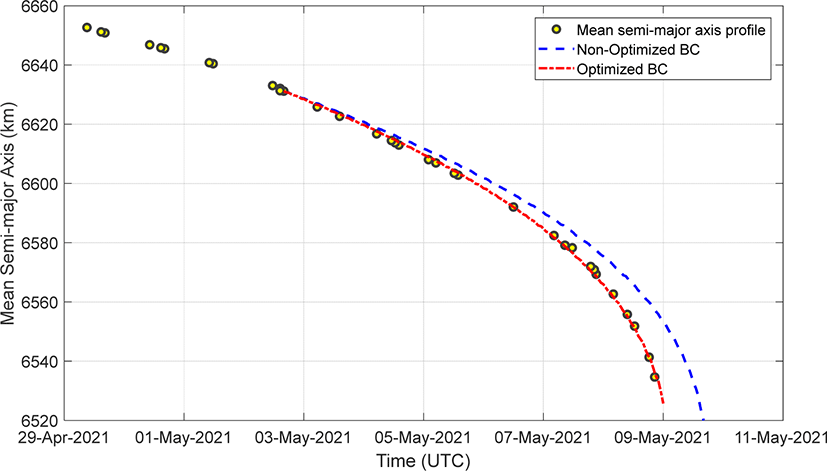
알려진 제원 정보를 이용하여 탄도계수를 계산할 수 있으나, 재진입 시점 예측 당시의 실제 물체의 상태(i.e., 연료의 양, 물체의 자세 등)를 알 수 없기 때문에 본 분석에서는 최적화 알고리즘을 적용하여 앞서 생성한 장반경 프로파일과 가장 잘 맞는 탄도계수를 탐색하였다. Fig. 2를 통해 최적의 탄도계수가 재진입 시점 예측에 미치는 영향을 확인할 수 있다. 여기서 일반 탄도계수(Non-Optimized BC)는 공유된 발사 전 물체의 상태를 기반으로 계산한 것이다.
본 최적화 과정에서는 패턴서치 알고리즘(Pattern Searching Method)을 이용하였다[19]. 패턴서치 알고리즘은 휴리스틱 알고리즘(Heuristic Algorithm)의 한 종류로서 주어진 환경에서 경험에 기반하여 최선의 해를 제공하는 방법이다. 그리드(grid)로 표현되는 탐색시점을 이동시키고 넓히거나 좁혀서 최적의 해를 탐색하는 방법으로 진화기반의 휴리스틱 알고리즘에 비해 비교적 탐색공간이 작은 문제에서 효과적으로 해를 탐색할 수 있으며, 본 연구에서는 단일 변수인 탄도계수만을 탐색하기 때문에 해당 알고리즘이 적합하다고 판단하였다. 해당 알고리즘 적용을 위해 MATLAB의 Global Optimization Toolbox를 사용하였다.
Table 1과 2는 궤도예측을 위한 섭동모델과 패턴서치 알고리즘의 설정치를 각각 나타낸다.
패턴서치 알고리즘이 임의의 탄도계수를 생성하면 TLE 데이터들 가운데 가장 오래된 TLE 데이터에서 궤도데이터를 생성하고, 이를 접촉궤도로 변환한다. 변환된 궤도와 생성된 탄도계수를 이용하여 가장 최신 TLE 데이터의 기산일까지 궤도예측을 수행하며, 궤도예측 결과로 나오는 시간에 대한 장반경을 앞서 생성한 기준 장반경과 비교한다.
식 (2)는 최적화를 위한 적합도 함수를 나타내며, 궤도예측 후 장반경 결과(api)와 기준 장반경(ari)의 평균 오차를 최소화하도록 문제를 정의하였다. 해당 식에서 도출하고자 하는 제어변수는 탄도계수이다.
N은 장반경 프로파일을 만들 때 사용된 TLE 데이터의 수를 의미한다. 장반경 프로파일 생성에 많은 수의 TLE 데이터를 적용하면 오관측된 TLE 데이터의 영향을 줄일 수 있으나, 재진입 물체의 특성상 고도가 낮아질수록 급격히 고도 하강률이 커지기 때문에 이와 같은 특성을 고려하는 데 불리한 부분이 있다. 따라서 재진입 대상물체의 특성에 따라 적절한 TLE 데이터 수를 고려하는 것이 필요하다.
최적화가 끝나면 최적화 과정에서 얻어낸 최종 탄도계수를 적용하여 물체의 고도가 80 km에 도달할 때까지 궤도예측을 수행하여 재진입 시점을 예측한다. 이 과정에서도 Table 2의 섭동모델을 동일하게 적용한다.
이후 시간이 흘러 새로운 TLE 데이터들이 배포되면 이상의 절차를 동일하게 반복하되, 장반경 프로파일 정의와 재진입 시점까지 궤도예측을 위한 TLE 데이터를 최신순으로 추출하여 적용한다. 장반경 프로파일 생성을 위해 10–20개의 TLE 데이터를 사용하는데, 이는 재진입 대상에 대한 세밀한 물성치 정보, TLE 데이터의 배포주기, 물체의 궤도 등을 고려하여 결정해야 한다. 장반경 프로파일 생성을 위해 많은 TLE 데이터를 적용할 경우, 오관측된 TLE 데이터의 영향을 줄일 수 있는 한편 재진입 시점이 가까워질 때 나타나는 급격한 고도 변화 등을 고려하기 어려운 단점이 존재한다. 하루에 배포되는 TLE의 수는 보통 2개 내외임을 고려하면 10–20개 TLE 데이터를 사용하는 것은 5–10일에 대한 데이터를 활용하는 것을 의미하며, 그 동안 재진입 캠페인을 수행하면서 얻은 경험적 수치이다.
Fig. 3은 이상의 과정을 플로우차트로 형태로 표현한 것이다.
3. 창정 5B호 발사체의 재진입 시점 예측 분석
2021년도 2차 IADC 재진입 분석 타깃인 창정 5B호 발사체는 2021년 4월 29일 중국 하이난섬의 원창 발사장에서 톈허 우주정거장 모듈을 위해 발사되었다. 중국 발사체 기술 아카데미가 개발한 창정 5호 발사체의 변형으로 발사 후 고도 170 km × 370 km 궤도에 남겨졌다. Fig. 4는 창정 5B 발사체의 형상을 보여주며, 제원에 대한 대략적인 정보는 너비 5 m, 높이 33.2 m, 질량은 18톤에 이르는 실린더 형태의 대형물체로서 1990년대 이후 가장 큰 규모의 비제어 재진입 사례이다.
Table 3은 재진입 분석에 대한 종합적인 정보를 나타낸다. 발사 직후부터 재진입까지 총 42개의 TLE 데이터가 배포되었고, 알려진 질량이나 크기, 형상 제원을 참고로 탄도계수 제한조건 및 초기조건을 정의하였다.
미국 연합우주작전센터(CSpOC, Combined Space Operations Center)에서 배포하는 TLE 데이터[21]를 이용하여 5월 5일부터 약 12시간 간격으로 5월 8일 21시까지 총 6회의 재진입 분석을 수행하였고, 각 분석 시 사용한 TLE 데이터, 분석 결과 도출된 재진입 시점, 잔여시간 대비 오차(상대오차)는 Table 4와 같다. 각 분석에서 달라지는 점은 장반경 프로파일 생성 및 최종 궤도예측에 사용되는 초기궤도 정보를 위한 TLE 데이터가 최신의 데이터로 교체되는 것이다. 분석결과에 대한 상대오차는 식 (3)과 같이 계산할 수 있다. tref)는 실제 재진입한 시점, t는 재진입 예측 결과, tp는 예측을 수행한 시점을 각각 의미한다.
분석은 약 12시간 간격으로 수행되었으며, 재진입 대상의 이심률이 0.015로 다소 큰 점과 높은 단면적으로 인한 대기저항의 불확실성을 고려하여 장반경 프로파일 생성에 최신의 TLE 데이터 10개만을 이용하여 각 분석을 수행하였다.
총 6회의 분석 결과, 탄도계수는 100.5102 kg/m2에서 106.5602 kg/m2까지 나타났고, 재진입 시점이 다가옴에 따라 장반경 프로파일과 최적 탄도계수를 적용한 궤도전파의 오차가 점차 증가하는 경향을 볼 수 있다. 이는 대기저항의 불확실성 영향으로 설정한 궤도예측 모델과 실제 관측 데이터인 TLE 데이터와의 차이가 점차 증가하는 것으로 해석할 수 있다. 예측구간 대비 정확도를 의미하는 상대오차의 경우 최소 분석 시 7.62%에서 점차 감소하여 마지막 분석에서는 0.36%로 나타났고, 절대오차의 경우 1.2분의 차이를 보여주어 재진입 예측 캠페인에 참여한 9개 기관의 평균 오차인 80분 대비 정확한 결과를 도출하였음을 확인하였다.
재진입 물체의 물성치나 초기궤도, 배포되는 TLE 데이터의 빈도, 주기에 따라 나타나는 재진입 시점예측의 오차는 달라질 수 있기에 절대적 기준의 오차를 정의하여 결과의 우수성을 평가하기보다 타 기관의 결과와 상대적 비교를 통해 제안한 분석기법의 성능을 가늠하는 것이 적절하다고 판단되며, 이러한 측면에서 본 연구에서 제안한 기법은 9개 기관 중 가장 정확한 결과이며, 평균 오차를 고려했을 때에도 우수한 결과를 보여주었다.
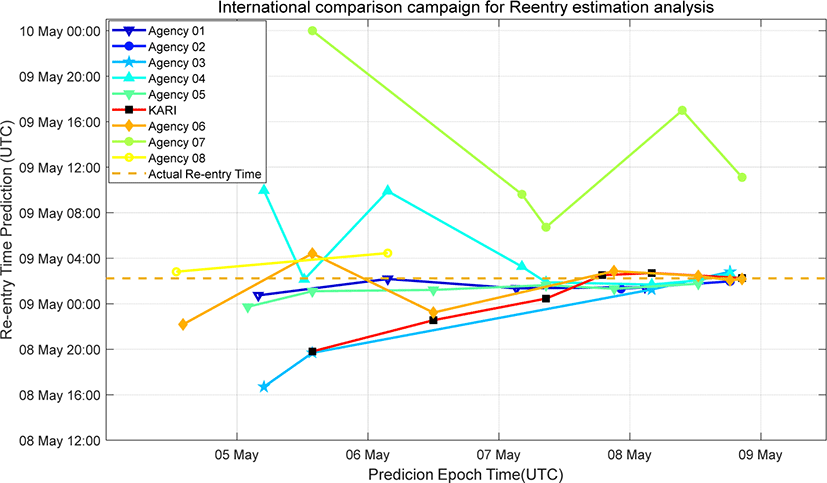
Fig. 5는 재진입 캠페인에 참여한 9개 기관의 재진입 분석 결과를 분석시간에 따라 나타낸 것이다. 캠페인 시작시점인 5월 5일 인근에서는 결과들의 분포가 상대적으로 넓게 나타나다가 일부 기관을 제외한 대부분의 기관의 경우 재진입 시점이 임박해감에 따라 점차 수렴되어 가는 모습을 볼 수 있다. 기관별 분석방법이나 사용하는 데이터에 따른 차이로 인한 결과의 차이는 예측을 수행하는 기간이 줄어듦에 따라 함께 감소하는 경향을 보여준다.
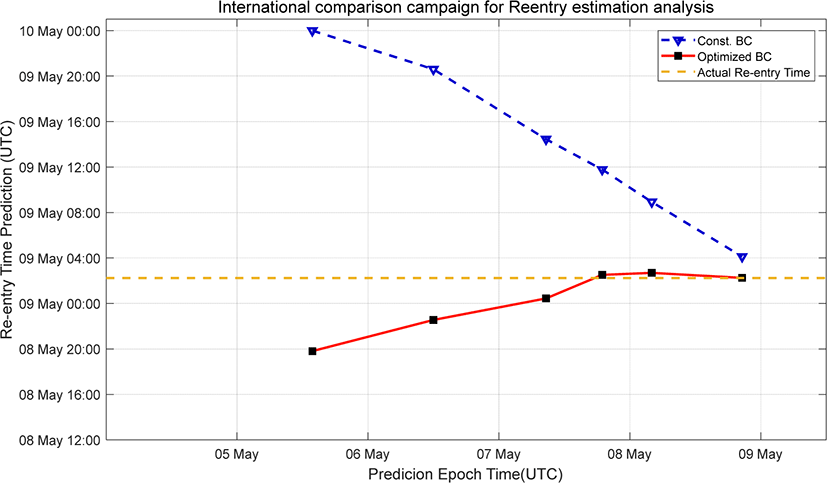
Fig. 6은 고정된 탄도계수(102.2727 kg/m2)를 적용했을 때와 매 분석 시 최적화된 탄도계수를 적용했을 때 재진입 시점 예측 정확도의 차이를 나타낸다. 고정된 탄도계수 사용 시 시간에 따라 실제 재진입 시점과의 차이가 점차 줄어드는 모습을 보여주지만, 최적 탄도계수 사용 결과 대비 큰 오차를 유지하고 있고, 최종 분석 결과는 5월 9일 4시 7분으로 나타나 113분의 오차를 보여주었다. 이를 통해 최적화된 탄도계수가 재진입 예측 정확도를 향상시킬 수 있음을 다시 한번 확인할 수 있다.
4. 결론
본 논문에서는 2021년 5월에 수행된 국제우주쓰레기조정위원회 재진입 테스트 캠페인의 분석 대상인 중국 창정 5B호 발사체의 재진입 시점 예측을 위해 탄도계수 최적화 기법을 제안하였다. 재진입 물체의 정확한 물리적 정보의 부재, 높은 이심률의 궤도와 TLE 데이터의 불확실성, 대기모델 등 섭동모델의 오차 등을 보상하기 위해 다수의 TLE 데이터를 이용하여 재진입 물체의 장반경 프로파일을 생성하고, 이를 잘 추종할 수 있는 탄도계수를 최적화 알고리즘으로 획득하여 재진입 예측에 적용하였다. 실제 중국 창정 5B 발사체 재진입에 제안한 기법을 적용하여 분석한 결과, 실제 재진입 시점과 불과 1.2분의 차이를 보여주었고, 이는 타 기관의 오차 평균인 80분 대비 정밀한 결과임을 확인하였다. 또한, 기존 알려진 불확실한 물리적 제원을 적용한 결과 대비해서도 우수한 결과를 확인하였다.
향후 오관측된 TLE 데이터가 분석결과에 미치는 영향과 이를 최소화하기 위한 연구나 기존 고려한 탄도계수뿐 아니라, 초기 궤도정보의 불확실성을 고려하는 방안, 다양한 불확실성 요소를 고려한 몬테칼로 시뮬레이션, 시간에 따른 탄도계수 변화 등을 고려한 후속 연구를 수행할 예정이다.