Your browser does not support the NLM PubReader view.

Go to this page to see a list of supporting browsers.
Journal of Space Technology and Applications
The Korean Space Science Society

J. Space Technol. Appl. 2025; 5(2):61-72

pISSN: 2765-7469

DOI: https://doi.org/10.52912/jsta.2025.5.2.61

연구논문

전자광학 탑재체의 2축 구동시스템에 대한 구조 안정성 연구

김항민1https://orcid.org/0009-0008-5772-8269, 차운용1https://orcid.org/0000-0001-9937-7585, 김진훈2https://orcid.org/0009-0004-2298-9638, 최동수2https://orcid.org/0009-0007-8195-5130, 오현웅1,3,†https://orcid.org/0000-0003-2161-7272
Study on the Safety of a Two-Axis Actuation System for an Electro-Optical Payload
Hang-Min Kim1https://orcid.org/0009-0008-5772-8269, Woon-Yong Cha1https://orcid.org/0000-0001-9937-7585, Jin-Hoon Kim2https://orcid.org/0009-0004-2298-9638, Dong-Soo Choi2https://orcid.org/0009-0007-8195-5130, Hyun-Ung Oh1,3,†https://orcid.org/0000-0003-2161-7272
1STEP Lab. Ltd.
2Justek
3한국항공대학교 항공우주 및 기계공학과
1STEP Lab. Ltd., Daejeon 34202, Korea
2Justek, Pyeongtack 17711, Korea
3Department of Aerospace and Mechanical Engineering, Korea Aerospace University, Goyang 10540, Korea
†Corresponding author : Hyun-Ung Oh, Tel : +82-2-300-0116, E-mail : ohu129@kau.ac.kr

© Copyright 2025 The Korean Space Science Society. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Feb 25, 2025; Revised: Mar 17, 2025; Accepted: Mar 19, 2025

Published Online: May 31, 2025

요 약

정지궤도 전자광학 탑재체 구동용 2축 구동시스템은 기존 임무의 승계 및 관측 성능 향상을 위해 적용된다. 본 연구에서는 설계하중 및 발사 충격환경, 궤도환경에서 2축 구동시스템의 구조 건전성을 확인하기 위해 구조해석을 실시하였다. 우선, 모드 해석을 통해 발사에서 구동시스템의 동적응답특성을 예측하였다. 또한 준정적 해석을 통해 구동시스템의 구조 건전성을 검토하였으며, 구동시스템과 위성체 간의 체결부 interface에 적용된 볼트에 대한 체결부 건전성을 검토하였다. 구동시스템의 경우 발사환경 하의 충격해석으로 구조 건전성을 확인하였다. 마지막으로 열응력 해석으로 궤도환경에서의 열적 구조 안전성을 검토하였다.

Abstract

The two-axis actuation system for the geostationary electro-optical payload is applied to succeed the existing mission and enhance observation performance. In this study, structural analysis was conducted to verify the structural safety of the two-axis actuation system under design loads, launch shock environments, and orbital conditions. First, a modal analysis was performed to predict the dynamic response characteristics of the drive system during launch. Additionally, a quasi-static analysis was conducted to evaluate the structural safety of the actuation system, and the integrity of the bolts used in the interface between the actuation system and the satellite body was examined. For the system, structural safety was verified through shock analysis under launch conditions. Finally, a thermal stress analysis was performed to assess the thermal structural safety of the system in an orbital environment.

Keywords: 2축 구동시스템; 구조해석; 유한요소해석; 모드해석; 준정적해석; 열응력해석
Keywords: two-axis actuation; structural analysis; finite element analysis (FEA); modal analysis; quasi-static analysis; thermal stress analysis

1. 서론

정지궤도 전자광학 탑재체의 구동시스템은 관측 성능 확보에 필수적인 동작 제어 기술이 요구되나, 현재는 해외 구매에 의존하고 있는 실정이다[1]. 이에 따라, 구동시스템의 기술 자립화 및 원천기술 확보를 위해 개발 중인 2축 구동시스템은 저궤도위성 대비 4.5초까지 노출 시간을 확대하여 복사성능을 향상시키는 반면 노출 시간 동안의 지향 포인트의 불안정성으로 인해 성능이 저하되어 2축 스캔 구동부의 지향 안정도가 필요하다. 이와 같이 2축 구동시스템은 위성체에 장착되어 발사 과정 및 정지궤도에 진입하기까지 발사체 및 위성체 분리에 의한 충격 하중, 발사체의 추진에 의한 정적 가속과 점화, 분리 과정에서의 동적 가속이 조합된 준정적 하중을 경험하게 된다. 또한 목표 궤도에 진입 후 탑재체는 우주의 열, 진공 환경에 노출되어 복사 및 전도에 의한 열 전달이 이루어진다[2,3]. 따라서 2축 구동시스템은 임무기간 동안 성공적인 임무 수행을 위해 상기 환경에서의 하중들로부터 구조건전성이 확보되도록 설계되어야 한다.

본 연구에서는 2축 구동시스템의 개요 및 구조해석 결과에 대해 기술하며, 발사 및 궤도 환경에서의 구조건전성 확보 여부를 검토하기 위해 유한요소모델(finite element model) 을 상용 구조해석 프로그램인 MSC Patran / hypermesh로 작성하였으며, Nastran을 solver로 사용하여 구조해석을 수행하였다. 우선적으로, 모드 해석을 수행하여 구동시스템의 동특성을 파악하고, 강성 요구조건 만족 여부를 검토하였다. 또한 준정적 해석을 수행하여 설계 하중 부가 시 구동시스템에 발생하는 응력에 대한 구조건전성 확보 및 체결부에서의 반력을 산출하여 체결부 구조건전성을 검토하였다. 추가로 발사 과정에서 탑재체가 경험하게 되는 충격에 대한 해석을 수행하여, 발사 환경 하 구동시스템의 구조건전성 확보 여부를 검토하였다. 마지막으로 궤도환경에서의 전도에 의한 열응력 해석으로 구동시스템의 열적 구조건전성을 검토하였다.

2. 본론

2.1 2축 구동시스템 구조해석 개요

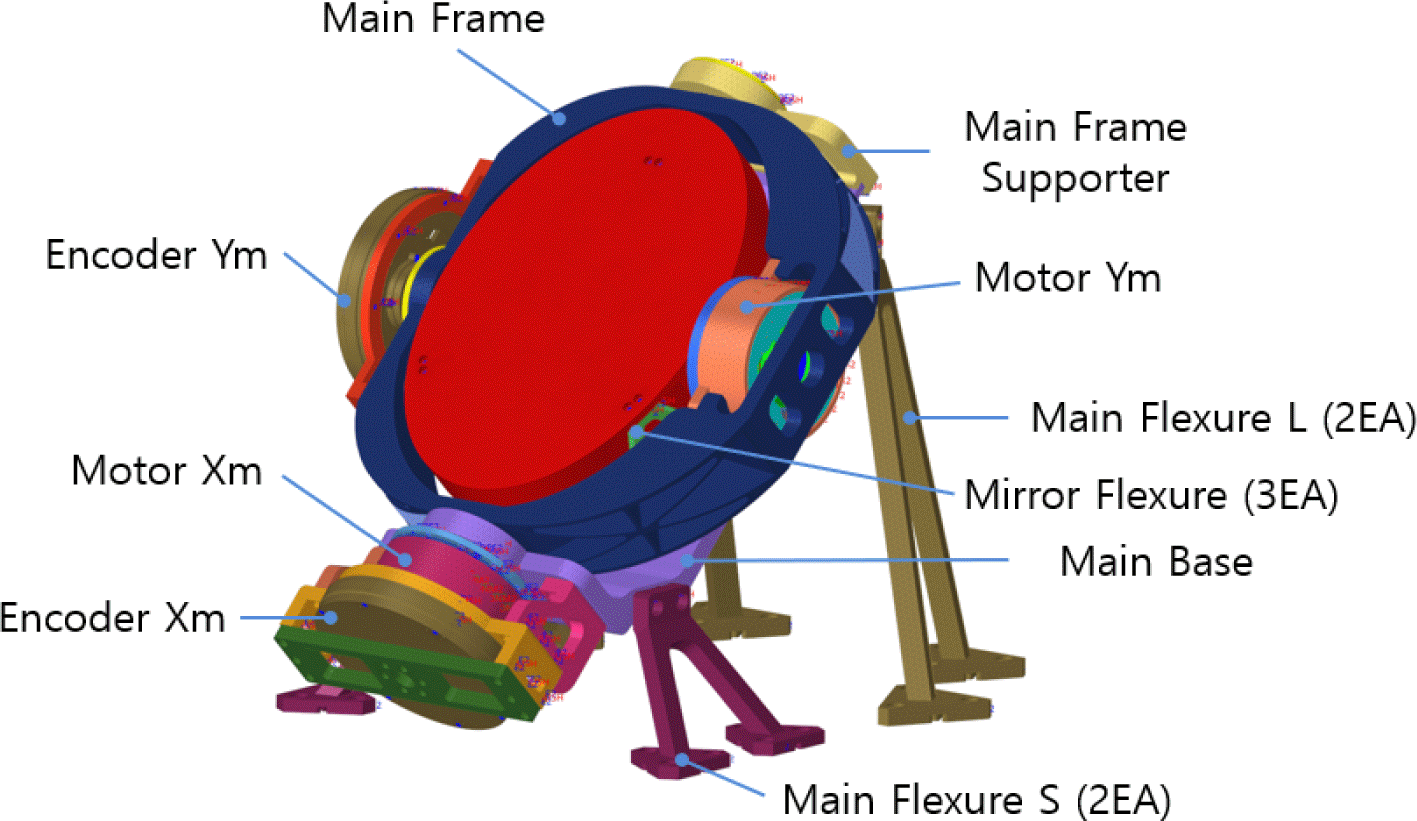
2축 구동시스템의 구조적 요구조건은 Table 1과 같으며, 요구조건에 대한 구조건전성 만족 여부를 검토하기 위하여 작성한 Fig. 1의 유한요소모델 무게는 약 29.6 kg이다. Table 2는 2축 구동시스템 유한요소모델 작성에 사용한 요소의 종류와 개수를 나타내며, 요소들은 구동시스템의 구성품 특성에 따라 적용되었다. 체결부의 경우 RBE2(rigid body element, Form2)와 CBUSH 요소를 조합하여 모사하였으며, 2축 구동시스템이 위성체와 장착되는 main flexure의 24개소의 체결부에 대해 6자유도(UX = UY = UZ = RX = RY = RZ = 0) 구속을 부여하였다. 회전 구동부의 볼 베어링은 상세 모델링 대신 RBE3(rigid body element, Form3)와 CBUSH 요소를 사용하여 단순화하였다. 발사 환경 시 볼 베어링은 구속되어 있는 상태이므로, CBUSH 강성은 강체로 모사하였다. 2축 구동시스템에 사용한 물성치는 Table 3에 나타내었으며, 작성한 유한요소모델의 적절성은 force balancing check로부터 검증하였으며, 구조체 중량에 대한 force 응답이 각 축별로 동일하게 도출됨을 확인하였다.

Table 1. Requirement for structural analysis
Classification Requirement
Stiffness 120 Hz ≤ Natural frequency
Strength Quasi-static 0 ≤ MoS
Shock 0 ≤ MoS
Thermoelastic 0 ≤ MoS
Download Excel Table
jsta-5-2-61-g1
Fig. 1. Finite element model of two-axis actuation system.
Download Original Figure
Table 2. Description of finite element model
Node or element Qty. Total qty.
Node 3,009,135 3,009,135
Element 1D RBE2 568 1,967,025
RBE3 16
CBUSH 223
CONM2 58
2D CQUAD4 15,077
3D CTETRA10 1,951,083

RBE2, rigid body element, Form2; RBE3, rigid body element, Form 3.

Download Excel Table
Table 3. Material properties for two-axis actuation system
Material Young’s modulus [GPa] Poisson’s ratio [-] Density [kg/m3]
Al6061-T651 68.3 0.33 2,700
Al7075-T6 71.7 0.33 2,800
SUS304 190.0 0.30 8,000
SUS440C 200.0 0.27 7,650
Ti-6Al-4V 113.8 0.34 4,430
Copper 110.0 0.34 8,930
Download Excel Table
2.2 2축 구동시스템 모드해석

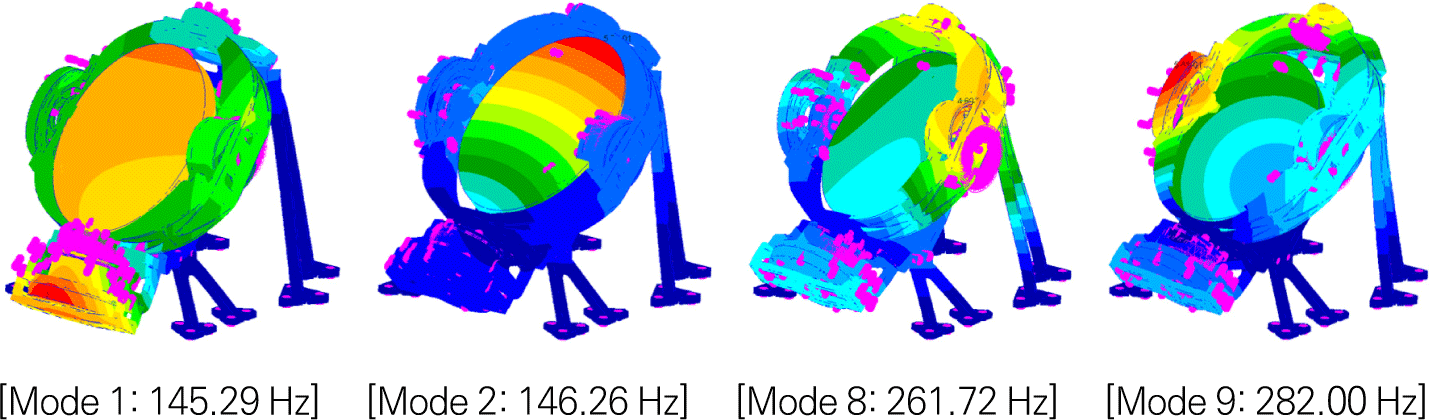
2축 구동시스템의 발사 환경에서의 동적 특성을 예측하려는 목적으로 Fig. 1의 유한요소모델을 사용하여, 모드 해석을 수행하였다. Fig. 2는 모드 해석 결과이며, 발사 환경에서 구조체는 탄성 거동하며, 고유진동수는 145.29 Hz로 구조체의 강성 요구조건을 만족함을 확인하였다.

jsta-5-2-61-g2
Fig. 2. Mode shape of two-axis actuation system.
Download Original Figure
2.3 2축 구동시스템 준정적 해석
2.3.1 2축 구동시스템

2축 구동시스템의 설계 하중에 대한 구조 건전성 검토를 위해 구조체 각 축 방향으로 30 g를 부가하여 구조체에 발생하는 최대 응력으로부터 안전여유(MoS)를 식 (1)을 통해 계산하였다.

MoS = σ a l l o w . S . F × σ m a x . − 1   ≥ 0
(1)

식 (1)에서의 σallow.은 재료의 허용 응력이며, σmax.는 구조해석 결과로 계산되는 최대응력, 그리고 S.F.는 안전계수로, 항복강도에 대해 1.25, 극한강도에 대해 1.40을 적용하였다[4]. Fig. 3은 준정적 해석 결과로 축 방향 별 설계하중 부가 시 구조체에 발생하는 최대 응력을 나타낸다. Table 4에서 작성한 바와 같이 각 축별 최대응력을 식 (1)로 안전여유를 계산한 결과를 정리한 것이며, 안전계수가 0 이상 값을 가지므로 설계 하중에 대해 구조체는 구조 건전성이 확보됨을 확인하였다.

jsta-5-2-61-g3
Fig. 3. Stress contour of the two-axis actuation system.
Download Original Figure
Table 4. Quasi-static analysis results for two-axis actuation system
Axis Component Material σyie. [MPa] σult. [MPa] σmax. [MPa] S.F. MoS
X Bearing holder SUS440C 450.0 760.0 113.1 Yie. 1.25 2.18
Ult. 1.40 3.79
Y Flexure Ti-6Al-4V 848.1 944.6 240.3 Yie. 1.25 0.49
Ult. 1.40 1.25
Z Dummy mirror Al6061-T651 276.0 310.0 156.4 Yie. 1.25 1.30
Ult. 1.40 2.47
Download Excel Table
2.3.2 체결부

2축 구동시스템의 설계 하중에 대한 탑재체와의 인터페이스 체결부 구조 건전성 검토를 위해 설계 하중 부가 시 체결부에서 계산되는 반력으로 안전계수를 계산하였다. 체결부에 적용된

볼트는 Tables 5, 6과 같이 Ti-6Al-4V 재질의 M8 볼트이며, Fig. 4는 구동시스템의 체결부 24개소에 대한 정의이다. 체결부에 사용된 볼트에 대한 구조 건전성 검토는 유한요소해석으로 산출된 X, Y, Z 방향의 반력으로부터 von-Mises stress 변환 후 안전여유를 식 (2)–(5)를 통해 계산하였다[5,6].

Table 5. Fastener information
Fastener type Material As [mm] Strength [MPa] S.F.
Yie. Ult. Yie. Ult.
M8 Ti-6Al-4V 36.6 848.1 944.6 1.25 1.40
Download Excel Table
Table 6. Fastener preload
Fastener type Material %yie. %uncrt. Preload [N]
P0 P0_min P0_max
M8 Ti-6Al-4V 0.6 0.1 18,227 16,404 20,049
Download Excel Table
jsta-5-2-61-g4
Fig. 4. Information for attachment on mounting interface.
Download Original Figure

Table 6은 적용 bolt에 대한 preload로 유한요소해석으로부터 산출한 볼트의 축 방향 하중에 합산하여 von-Mises 응력을 계산하여 구조건전성 평가에 적용하였다[6]. Table 7은 볼트 구조건전성 평가로 각 축 방향 설계하중(30 g) 부가 시 보수적으로 반력의 최대값을 사용하여 식 (5)와 같이 검토하였으며, 안전계수가 0 이상의 값을 가져 체결부에서의 구조 건전성이 확보됨을 확인하였다.

Table 7. Bolt analysis results
No. Fastener shear [N] Fastener axial [N] Max. fastener stress [MPa] MoS
X Y Z X Y Z Yie. Ult.
1 2,697 1,771 1,217 1,706 1,327 674 608 0.09 0.05
2 1,246 774 1,396 838 757 921 576.8 0.15 0.11
3 601 904 107 410 837 3 572.3 0.16 0.12
4 1,768 1,451 694 1,155 1,065 522 585.4 0.13 0.09
5 220 982 313 148 802 242 571.6 0.16 0.12
6 934 282 169 690 255 142 568.4 0.16 0.13
7 958 328 180 887 345 185 573.8 0.15 0.12
8 380 130 78 512 63 99 562.1 0.18 0.14
9 104 117 233 122 175 305 556.3 0.19 0.15
10 437 737 269 410 713 234 568.4 0.16 0.13
11 345 525 123 691 315 15 567.2 0.17 0.13
12 651 572 537 1,182 306 849 580.9 0.14 0.10
13 2,839 1,802 1,125 1,806 1,342 591 612.1 0.08 0.05
14 1,243 819 1,405 837 789 904 576.4 0.15 0.11
15 636 867 87 432 813 15 571.5 0.16 0.12
16 1,962 1,435 752 1,283 1,060 539 590.2 0.12 0.08
17 313 934 385 219 766 296 570.4 0.16 0.12
18 1,015 312 208 743 276 171 570.1 0.16 0.12
19 1,087 293 209 1,016 315 207 577.9 0.14 0.11
20 428 134 109 564 99 140 563.6 0.17 0.14
21 129 89 269 147 138 349 557.5 0.19 0.15
22 538 699 352 513 679 314 567.3 0.17 0.13
23 380 539 97 764 340 118 569.2 0.16 0.12
24 663 558 595 1,220 277 910 582 0.14 0.10
Download Excel Table
F a s t e n e r   A x i a l = ( F z ) 2
(2)
F a s t e n e r   S h e a r = ( F x ) 2 + ( F y ) 2
(3)
σ F a s t e n e r = ( ( F a s t e n e r   A x i a l   +   P 0 _ M a x A s ) 2 + 3 × ( F a s t e n e r   S h e a r A s ) 2
(4)
MoS = σ a l l o w . S . F × σ F a s t e n e r − 1   ≥ 0
(5)
2.4 2축 구동시스템 충격해석

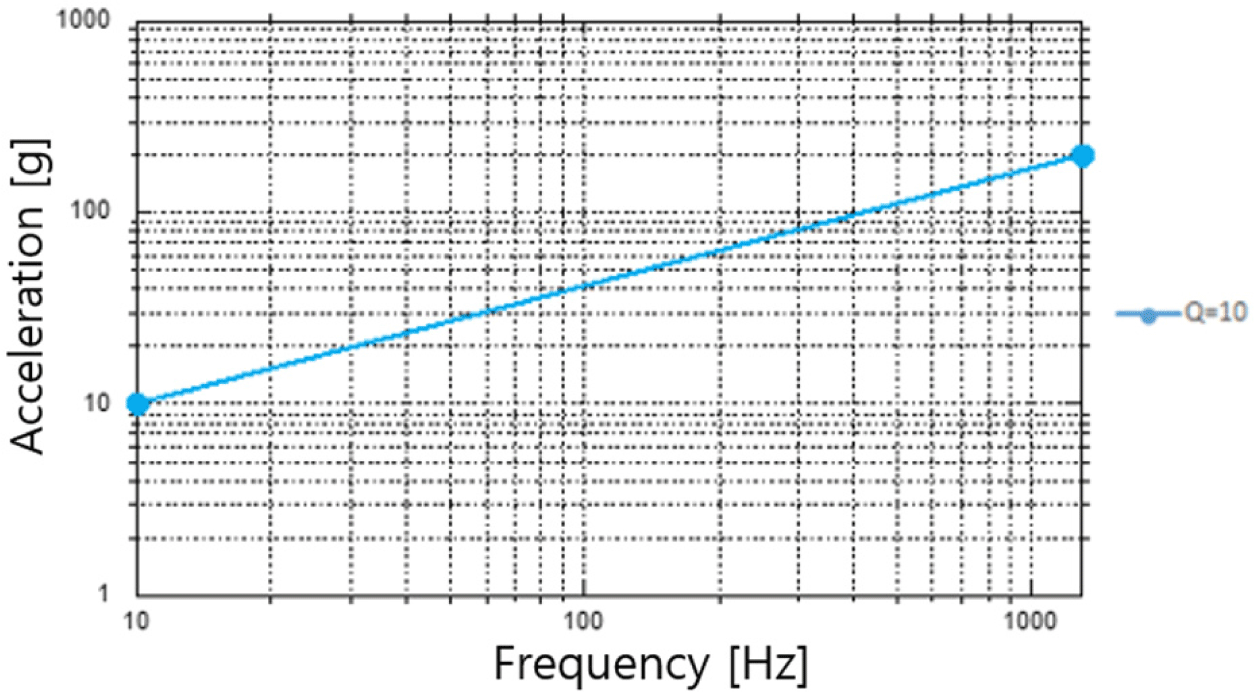
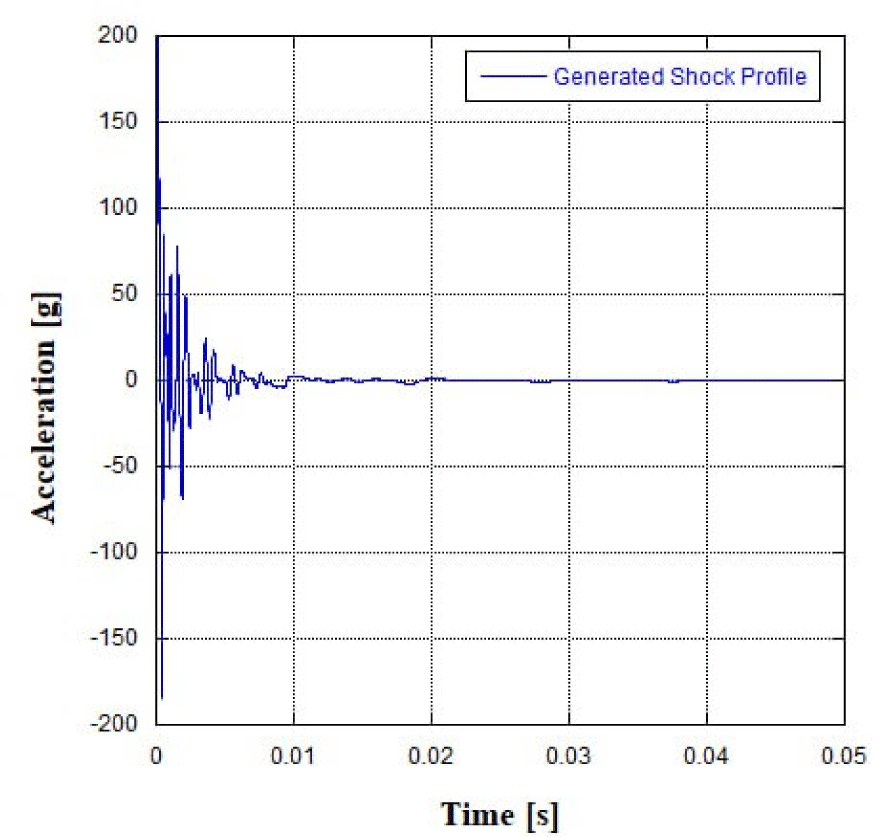
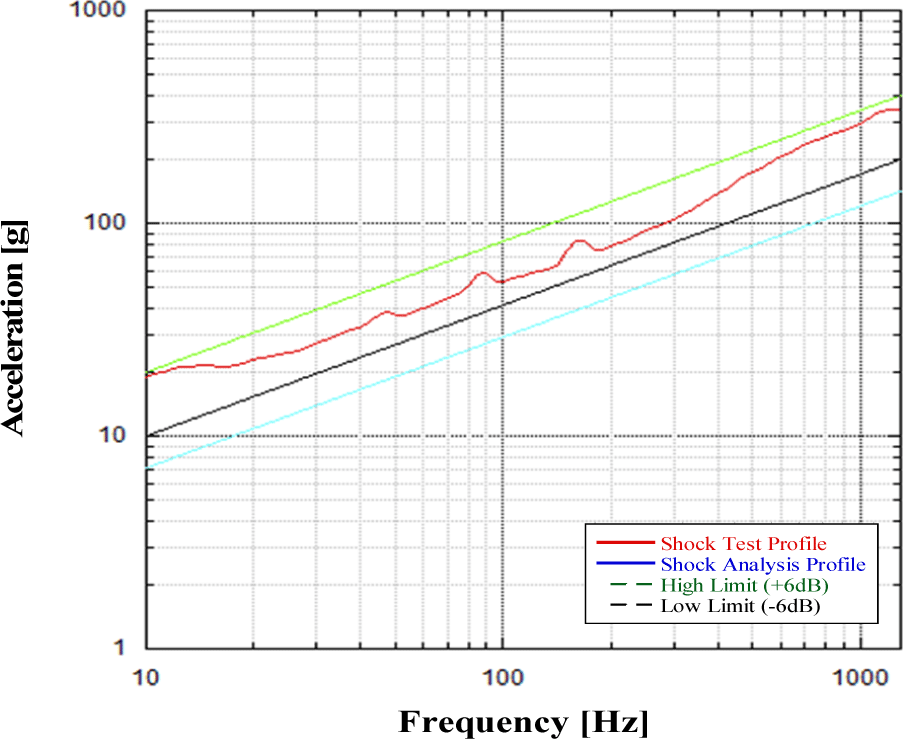
2축 구동시스템의 발사과정에서 시스템이 경험하는 충격 하중에 대한 구조건전성 검토를 목적으로 한다. 충격 하중에 대한 정보는 상위 연구기관에서 제공받은 정보이며, Fig. 5와 Table 8과 같다. 충격하중은 매우 짧은 시간 동안 작용하는 하중으로 이를 해석적으로 모사하기 위해 모드 과도 해석(modal transient analysis) 수행하였다. 본 해석에서는 SRS(shock response spectrum)를 기반으로 하여 임의의 시간 영역에서의 가속도 응답을 도출하였다. 도출된 가속도 응답은 Fig. 6에 제시되어 있으며, 시간 영역에서의 입력 파형은 감쇠된 정현파(damped sinusoids)의 조합으로 합성하였다. 감쇠된 정현파를 조합하는 방식은 다양한 주파수 성분을 포함할 수 있어 충격 하중의 특성을 보다 정확하게 모사하는데 유용하다. 이를 통해 구조물의 동적 거동을 보다 정확하게 예측하고자 하였다[7]. 도출 규격의 타당성 검증을 위해 SRS를 Fig. 7과 같이 재산출 하였으며, 시험 규격인 +6–0 dB 내 profile이 위치하여 규격과 유사한 경향성을 나타냄을 확인하였다.

jsta-5-2-61-g5
Fig. 5. Shock input profile.
Download Original Figure
jsta-5-2-61-g6
Fig. 6. Acceleration-time curve base on shock response spectrum.
Download Original Figure
jsta-5-2-61-g7
Fig. 7. Shock test & analysis shock response spectrum.
Download Original Figure
Table 8. Shock analysis specification
Frequency [Hz] Acceleration [g]
10 10
1,300 200
Download Excel Table

SRS 기반으로 time domain profile을 적용한 축 방향 별 충격해석의 결과는 Fig. 8과 같으며, 구조체의 발생하는 최대 응력을 식 (1)을 통해 안전여유를 계산한 결과는 Table 9에 정리하였다. 안전계수가 0 이상의 값을 가지므로 2축 구동시스템은 충격하중에서 구조건전성이 확보 가능할 것으로 판단된다.

jsta-5-2-61-g8
Fig. 8. Shock analysis results.
Download Original Figure
Table 9. Shock analysis results for two-axis actuation system
Axis Component Material σyie. [MPa] σult. [MPa] σmax. [MPa] S.F. MoS
X Bracket Al6061-T651 276.0 310.0 73.4 Yie. 1.25 2.00
Ult. 1.40 2.01
Y Flexure Ti-6Al-4V 848.1 944.6 237.4 Yie. 1.25 1.85
Ult. 1.40 1.84
Z Yoke Ym SUS440C 450.0 760.0 132.8 Yie. 1.25 1.71
Ult. 1.40 3.08
Download Excel Table
2.5 2축 구동시스템 열응력해석

상온(약 20℃)에서 조립된 2축 구동시스템은 Non-Operation(–20℃–+55℃)의 온도 환경 조건에서 구조건전성을 검토하였다. 실제 온도차는 ΔT는 35℃이나, 보수적인 해석을 위해 40℃의 조건을 구조해석에 적용하였다. 2축 구동시스템의 적용된 물성은 등방성 물성으로 선형적인 온도 변화를 가지며, 온도 변화에 의해 물체 내부에서 발생하는 열응력은 식 (6)에 따르며 초기 온도 기준 1℃ 차이를 준 선형 해석 이후 결과를 선형 보간하여 결과를 도출하였다.

σ T = Eα Δ T
(6)

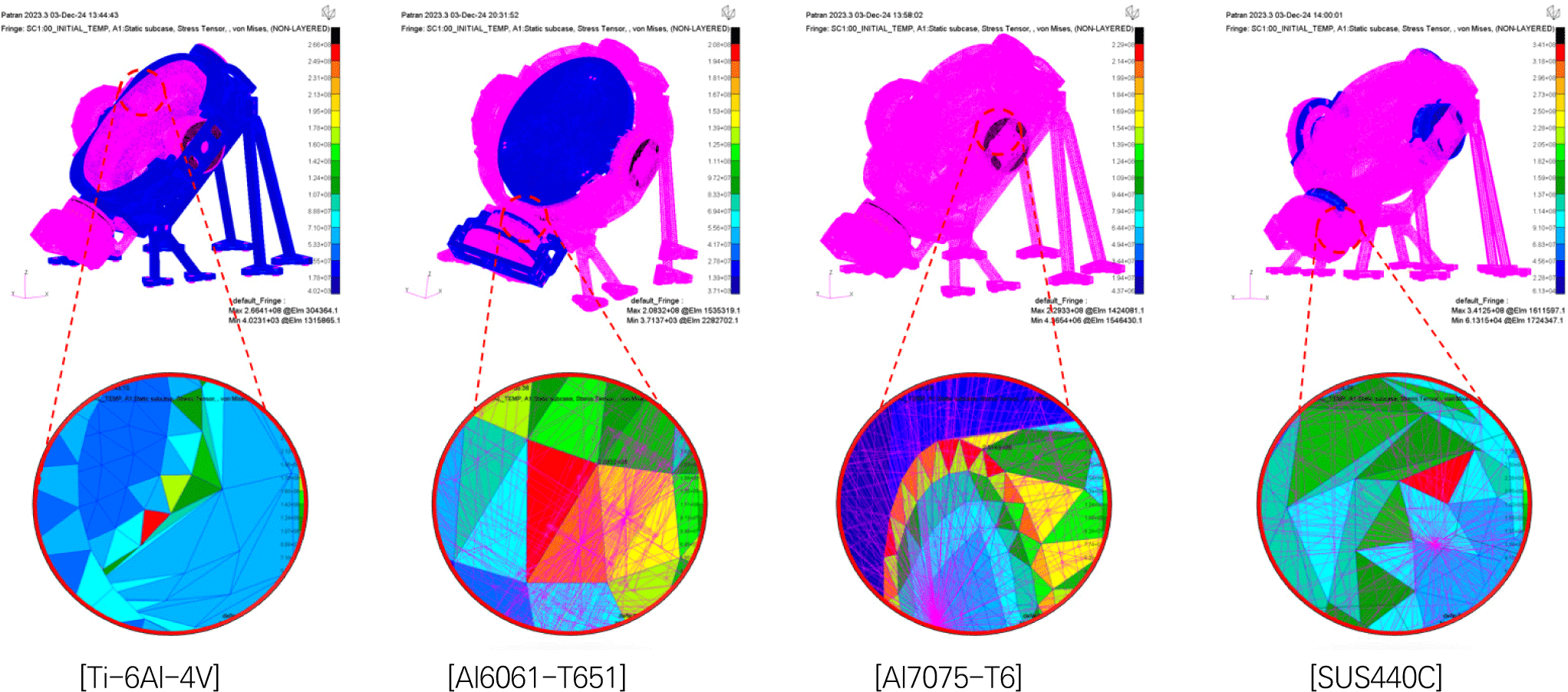
열응력 해석 결과는 Fig. 9와 같으며, 온도 변화에 의해 구조체 내부에서 발생하는 최대 열응력을 식 (1)을 통해 안전여유를 계산한 결과를 물성 별 결과로 Table 10에 정리하였다. 2축 구동시스템의 온도 환경보다 보수적인 해석 수행 결과로 안전계수가 0 이상의 값을 가지며 이는 구조체의 열적 구조안전성이 확보됨을 확인하였다.

jsta-5-2-61-g9
Fig. 9. Thermal stress analysis results.
Download Original Figure
Table 10. Thermal stress analysis results for two-axis actuation system
Component Material σyie. [MPa] σult. [MPa] σmax. [MPa] S.F. MoS
Main frame Ti-6Al-4V 848.1 944.6 266.4 Yie. 1.25 1.54
Ult. 1.40 1.53
Rotation plate Xm Al6061-T651 276.0 310.0 208.3 Yie. 1.25 0.06
Ult. 1.40 0.07
Shaft Ym Al7075-T6 503.0 572.0 231.4 Yie. 1.25 0.73
Ult. 1.40 0.76
Yoke Xm SUS440C 450.0 760.0 341.3 Yie. 1.25 0.05
Ult. 1.40 0.59
Download Excel Table

3. 결론

본 논문에서는 정지궤도 전자광학 탑재체의 2축 구동시스템에 대한 구조 건전성 검토를 위해 구조해석을 수행하였다. 구조해석은 모드해석, 준정적해석, 충격해석, 열응력 해석 총 4 항목을 수행하였으며, 모드 해석 결과 2축 구동시스템의 고유진동수 요구조건인 120 Hz 이상을 만족함을 확인하였다. 또한 준정적해석 수행 결과로 허용응력 대비 구조체에 발생하는 응력에 대한 안전여유를 산출하여 설계하중에 대한 구조체의 구조건전성 및 준정적해석으로 계산되는 체결부에서의 반력으로 구조체와 위성체 간 체결부의 구조 건전성 역시 확보됨을 확인하였다. 2축 구동시스템이 발사간 경험하는 충격하중에 대한 충격해석을 수행하여 충격하중에서의 구조건전성을 확인하였으며, 궤도 환경에서의 온도 조건에 대한 열응력 해석 수행으로 온도 변화에 대한 구조체의 구조건전성을 확인하였다.

감사의 글

본 연구는 과학기술정보통신부의 거대과학연구개발사업인 ‘스페이스 파이오니어사업’에 의해 수행되었습니다(세부과제번호: 2021M1A3B9094415).

References

1.

Song BS, Suk BS, Park SM, Shim YJ, Yong SS, et al., The space key technology development trend through Korea space pioneer program, Curr. Ind. Technol. Trends Aerosp. 21, 112-120 (2023).

2.

Jeon SH, Kwon SC, Kim TH, Oh HU, Enhancement of microjitter attenuation capability for a stepper-actuated two-axis gimbal-type antenna by using a spring-blade isolator, J. Aerosp. Eng. 30, 04017017 (2017).

3.

Jeong SY, Oh HU, Lee KJ, Kim BS, Mechanical stability analysis of PCB and component for launch and on-orbit environment based on fatigue failure theory and FEM, J. Korean Soc. Aeronaut. Space Sci. 39, 952-958 (2011).

4.

Space Engineering, Mechanisms (European Cooperation for Space Standardization, Noordwijk, the Netherlands, 2009).

5.

Space Engineering, Threaded Fasteners Handbook (European Cooperation for Space Standardization, Noordwijk, the Netherlands, 2010).

6.

Steeve BE, Wingate RJ, Aerospace threaded fastener strength in combined shear and tension loading (2012) [Internet], viewed 2025 Feb 26, available from: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nsa.gov

7.

Irvine T, Shock Response Spectrum Synthesis via Damped Sinusoids Revision B (Vibrationdata, Catarina Mesa, AZ, 2012).

Author Information

김 항 민hmkim@steplab.co.kr

jsta-5-2-61-i1

전북대학교 기계설계공학부에서 2018년 학사학위를 취득한 후, 2019년부터 ANH Structure에서 회전익 구조설계, 해석 업무를 수행하였다. 현재는 ㈜스텝랩에서 위성체 구조해석 및 연구를 수행하고 있다.

최 동 수dschoi@justek.com

jsta-5-2-61-i2

서울대학교 전기공학부에서 1996년 학사학위를 취득한 후, 서울대학교 전기컴퓨터공학부에서 1998년과 2002년에 각각 석사와 박사학위를 취득하였다. 현재는 ㈜져스텍에서 대표이사로 재직하고 있으며, 연구분야는 비선형 제어 이론을 응용한 리니어모터의 고정밀 자세 제어이다.

김 진 훈jhkim@justek.com

jsta-5-2-61-i3

부산대학교 기계공학과에서 1996년 학사학위를 취득한 후, ㈜삼성전기에서 수석연구원으로 근무하였다. 현재는 ㈜져스텍에서 수석연구원으로 재직하고 있으며, 연구분야는 위성용 구동부 개발업무를 수행하고 있다.

차 운 용wycha@steplab.co.kr

jsta-5-2-61-i4

선문대학교 기계공학과에서 동역학 및 기계진동 전공으로 박사학위를 취득하였으며, 2012년부터 엠에이치에스에서 ANSYS와 Recur-Dyn을 활용하여 구조/동역학에 대한 해석 및 연구를 수행하였다. 현재는 ㈜스텝랩에서 위성체 기계시스템, 우주용 메커니즘 등 다양한 연구를 수행하고 있다.

오 현 웅ohu129@kau.ac.kr

jsta-5-2-61-i5

1992년 한국항공대학교 항공우주공학 학사학위, 동 전공으로 일본 동경대학교에서 1997년 석사학위, 1999년 박사학위를 취득했다. JAXA(1999–2005), 국방과학연구소(2005–2012)에서 연구원으로 근무하였으며, 조선대학교(2012–2023) 스마트이동체융합시스템공학부 교수로 위성시스템 분야 연구를 수행하였다. 현재 한국항공대학교 항공우주공학과 교수로 재직중이며, 위성/탑재체 기계시스템, 초소형위성, 진동제어 등 다양한 연구를 수행하고 있다.